Câu hỏi:
89 lượt xem Tự luận
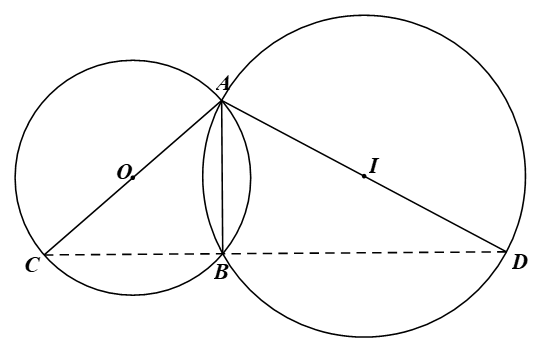
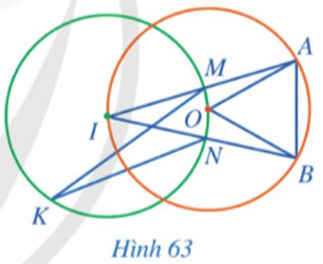
Cho hai đường tròn (O), (I) cắt nhau tại hai điểm A, B. Kẻ các đoạn thẳng AC, AD lần lượt là các đường kính của hai đường tròn (O), (I). Chứng minh ba điểm B, C, D thẳng hàng.
Lời giải
Hướng dẫn giải:
Ta có:
⦁ ˆABC=90°(góc nội tiếp chắn nửa đường tròn (O)).
⦁ ˆABD=90° (góc nội tiếp chắn nửa đường tròn (I)).
Suy ra ˆABC+ˆABD=90°+90°=180° hay ˆCBD=180°.
Do đó ba điểm B, C, D thẳng hàng.
Câu 1:
Câu 2:
Tự luận
Cho đường tròn (O). Hãy vẽ góc xOy có đỉnh là tâm O của đường tròn đó.
1 năm trước
61 lượt xem
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 9:
Câu 10:
Câu 11:
Tự luận
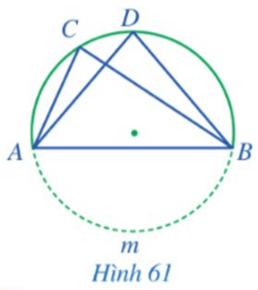
Trong Hình 61, gọi I là giao điểm của AD và BC. Chứng minh IA.ID = IB.IC.
1 năm trước
105 lượt xem
Câu 12:
Câu 13:
Câu 14:
Câu 15:
Câu 17: