Câu hỏi:
115 lượt xem Tự luận
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) trên đoạn [-1;3]
b) trên đoạn [3;11]
c) trên đoạn [3;7]
d) trên đoạn
Lời giải
Hướng dẫn giải:
a) Xét trên đoạn [-1;3]
Bảng biến thiên:
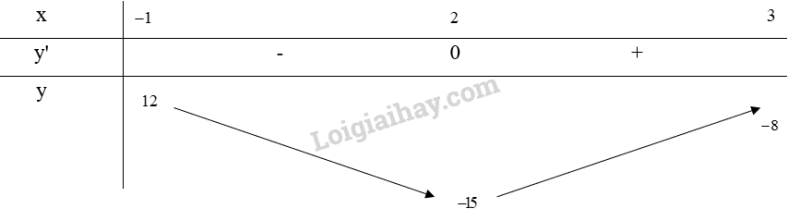
Từ bảng biến thiên, ta thấy và
b) Xét trên đoạn [3;11]
Bảng biến thiên:
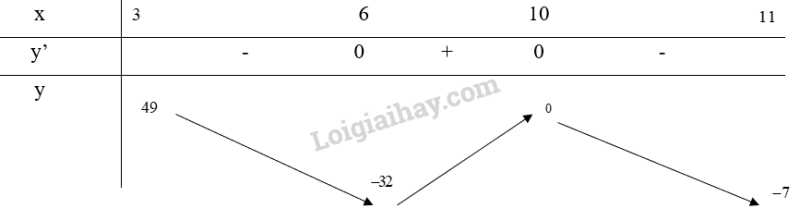
Từ bảng biến thiên, ta thấy và
c) Xét trên đoạn [3;7]
Bảng biến thiên:
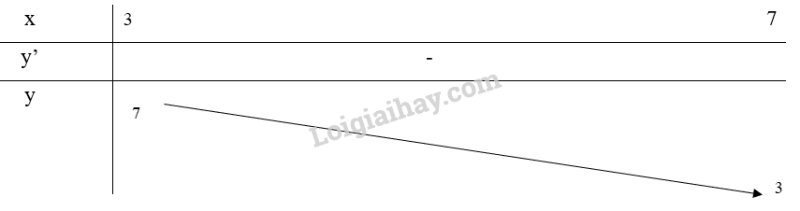
Từ bảng biến thiên, ta thấy và
d) Xét trên đoạn
Ta có:
Bảng biến thiên:
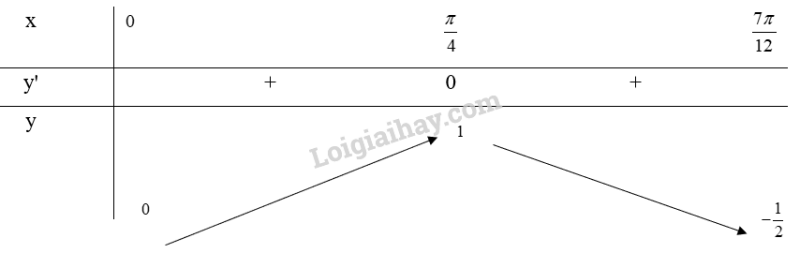
Từ bảng biến thiên, ta thấy và
Câu 2:
Câu 4:
Câu 5:
Câu 6:
Tự luận
Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?
1 năm trước
108 lượt xem
Câu 7:
Tự luận
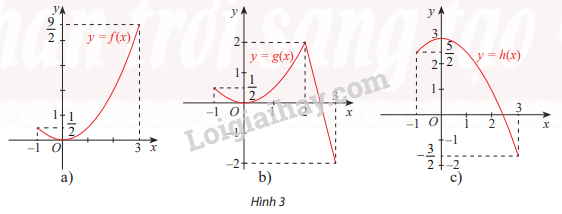
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5
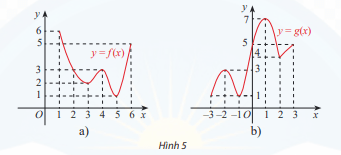
1 năm trước
84 lượt xem
Câu 9:
Câu 10:
Câu 11: