Câu hỏi:
116 lượt xemGiải bài tập Toán 10 Bài tập cuối chương 3
A. Trắc nghiệm
Giải Toán 10 trang 44 Tập 1
Bài 3.12 trang 44 Toán 10 Tập 1: Cho tam giác ABC có . Khẳng định nào sau đây là đúng?
a)
A.
B.
C.
D.
b)
A.
B.
C.
D.
c)
A. .
B.
C.
D. b2 = c2 + a2 – 2ca.cos135o.
Lời giải
Hướng dẫn giải:
Lời giải:
Tam giác ABC có BC = a; AC = b; AB = c; .
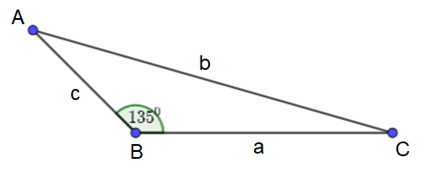
a) Diện tích tam giác ABC:
.
Chọn D.
b) Theo định lí sin, ta có:
A. sai vì
B.
Mà .
Do đó B đúng.
C. (loại vì không có dữ kiện về góc C nên không thể tính R theo c).
D. (loại vì không có dữ kiện về góc A nên không thể tính R theo a).
Chọn B.
c)
A. .
Vì theo định lí côsin, ta có: a2 = b2 + c2 − 2bc . cosA
Không đủ dữ kiện để suy ra: .
Do đó A sai.
B. .
Theo định lí sin, ta có:
Nên .
Do đó B sai.
C. .
Vì theo câu a, .
Do đó C sai.
D. b2 = c2 + a2 – 2ca . cos135o. đúng.
Theo định lý côsin ta có:
b2 = c2 + a2 − 2ca . cosB (*)
Mà cosB = cos 135o.
Thay vào (*) ta được: b2 = c2 + a2 − 2ca . cos 135o.
Do đó D đúng.
Chọn D.
Bài 3.15 trang 44 Toán 10 Tập 1: Cho tam giác ABC có AC = 10. Tính a, R, S, r.