Câu hỏi:
183 lượt xemBài 5.15 trang 88 Toán 10 Tập 1: Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):
2,977 3,155 3,920 3,412 4,236
2,593 3,270 3,813 4,042 3,387.
Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu này.
Lời giải
Hướng dẫn giải:
Sắp xếp các giá trị của số liệu trên theo thứ tự từ không giảm là:
2,593; 2,977; 3,155; 3,270; 3,387; 3,412; 3,813; 3,920; 4,042; 4,236.
Ta có giá trị lớn nhất là 4,236 kg và giá trị nhỏ nhất là 2,593 kg.
Khi đó, khoảng biến thiên là: R = 4,236 – 2,593 = 1,643.
Vì n = 10 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa:
Q2 = (3,387 + 3,412) : 2 = 3,3995.
Nửa số liệu bên trái gồm 5 số liệu là một số lẻ nên tứ phân vị thứ nhất là: Q1 = 3,155.
Nửa số liệu bên phải gồm 5 số liệu là một số lẻ nên tứ phân vị thứ ba là: Q3 = 3,920.
Khoảng tứ phân vị là: ∆Q = Q3 – Q1 = 3,920 – 3,155 = 0,765.
Số trung bình cộng của mẫu số liệu là:
Ta có bảng sau:
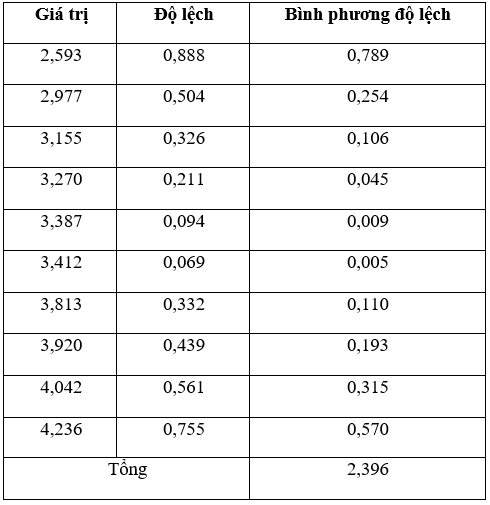
Phương sai:
Độ lệch chuẩn: .
Vậy khoảng biến thiên R = 1,643, khoảng tứ phân vị độ lệch chuẩn s ≈ 0,489.