Câu hỏi:
79 lượt xemCho cos α = , sin α > 0; sin β = , . Hãy tính cos 2α, sin 2α, cos 2β, sin 2β, cos (α + β), sin (α – β).
Lời giải
Hướng dẫn giải:
Ta có cos 2α = 2 cos2 α – 1 = .
Ta có sin2 α = 1 – cos2 a = = .
Lại do sin α > 0 nên sin α = .
Suy ra sin 2α = 2 sin α cos α = .
Ta có cos 2β = 1 – 2 sin2 β = = .
Ta có cos2 β = 1 – sin2 β = = .
Lại do nên cos β < 0, do đó .
Suy ra sin 2β = 2 sin β cos β = .
Ta có
cos(α + β) = cos α cos β – sin α sin β = .
sin(α – β) = sin α cos β – cos α sin β = .
Giá trị của các hàm số y = sin3x và y = sin x bằng nhau khi và chỉ khi
Chứng minh các biểu thức sau không phụ thuộc vào x:
a) ;
b) ;
c) ;
d) .
Tìm tập xác định của các hàm số sau:
a) ;
b) ;
c) ;
d) y = tan x + cot x.
Xét tính tuần hoàn của các hàm số sau:
a) y = sin + cos 3x;
b) y = cos 5x + tan.
Giải các phương trình sau:
a) ;
b) ;
c) sin 3x – cos 5x = 0;
d) tan 3x tan x = 1.

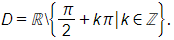
![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1.PNG) là
là