Câu hỏi:
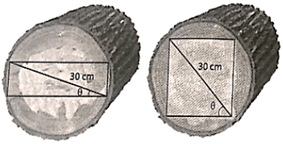
93 lượt xemMột thanh xà gồ hình hộp chữ nhật được cắt ra từ một khối gỗ hình trụ có đường kính 30 cm.
a) Chứng minh rằng diện tích mặt cắt của thanh xà gồ được tính bởi công thức
S(θ) = 450 sin 2θ (cm2),
ở đó góc θ được chỉ ra trong hình vẽ dưới đây.
b) Tìm góc θ để diện tích mặt cắt của thanh xà gồ là lớn nhất.
Lời giải
Hướng dẫn giải:
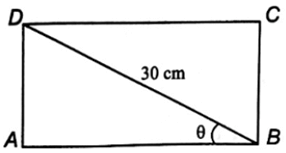
a) Mặt cắt của thanh xà gồ (hình dưới) là hình chữ nhật có hai kích thước là
AB = 30cos θ và BC = 30sin θ.
Vậy diện tích mặt cắt là S = AB ∙ BC = 30cos θ ∙ 30sin θ = 450sin 2θ.
b) Vì – 1 ≤ sin 2θ ≤ 1 nên ta có S = 450sin 2θ ≤ 450.
Vậy diện tích mặt cắt của thanh xà gồ lớn nhất khi sin 2θ = 1 hay góc θ = 45°.
Giá trị của các hàm số y = sin3x và y = sin x bằng nhau khi và chỉ khi
Chứng minh các biểu thức sau không phụ thuộc vào x:
a) ;
b) ;
c) ;
d) .
Tìm tập xác định của các hàm số sau:
a) ;
b) ;
c) ;
d) y = tan x + cot x.
Xét tính tuần hoàn của các hàm số sau:
a) y = sin + cos 3x;
b) y = cos 5x + tan.
Giải các phương trình sau:
a) ;
b) ;
c) sin 3x – cos 5x = 0;
d) tan 3x tan x = 1.

![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1.PNG) là
là