Câu hỏi:
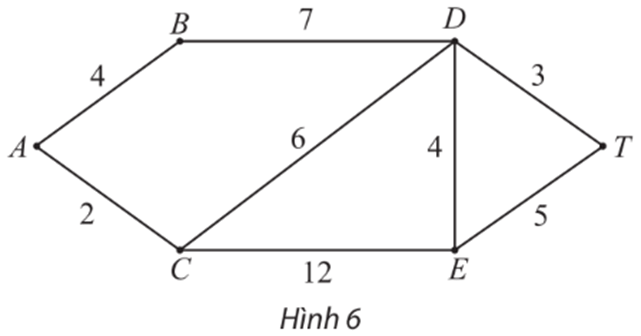
130 lượt xemCho đồ thị có trọng số như Hình 6.
a) Tìm tất cả các đường đi từ A đến T (đi qua mỗi đỉnh nhiều nhất một lần) và tính độ dài của mỗi đường đi đó.
b) Từ đó, tìm đường đi ngắn nhất từ A đến T.
Lời giải
Hướng dẫn giải:
a) Tất cả các đường đi từ A đến T (đi qua mỗi đỉnh nhiều nhất một lần) là: ABDT, ACDT, ACET, ACDET, ACEDT, ABDET, ABDCET.
Ta có:
⦁ lABDT = wAB + wBD + wDT = 4 + 7 + 3 = 14;
⦁ lACDT = wAC + wCD + wDT = 2 + 6 + 3 = 11;
⦁ lACET = wAC + wCE + wET = 2 + 12 + 5 = 19;
⦁ lACDET = wAC + wCD + wDE + wET = 2 + 6 + 4 + 5 = 17;
⦁ lACEDT = wAC + wCE + wED + wDT = 2 + 12 + 4 + 3 = 21;
⦁ lABDET = wAB + wBD + wDE + wET = 4 + 7 + 4 + 5 = 20;
⦁ lABDCET = wAB + wBD + wDC + wCE + wET = 4 + 7 + 6 + 12 + 5 = 34.
b) Vì 11 < 14 < 17 < 19 < 20 < 21 < 34.
Nên lACDT < lABDT < lACDET < lACET < lABDET < lACEDT < lABDCET.
Vậy đường đi ngắn nhất từ A đến T là ACDT (có độ dài bằng 11).
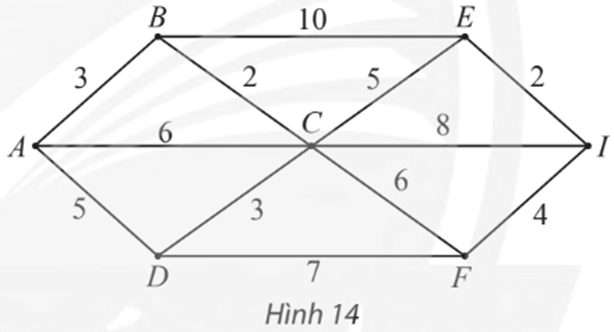
Tìm đường đi ngắn nhất từ đỉnh A đến đỉnh I trong đồ thị có trọng số ở Hình 14.
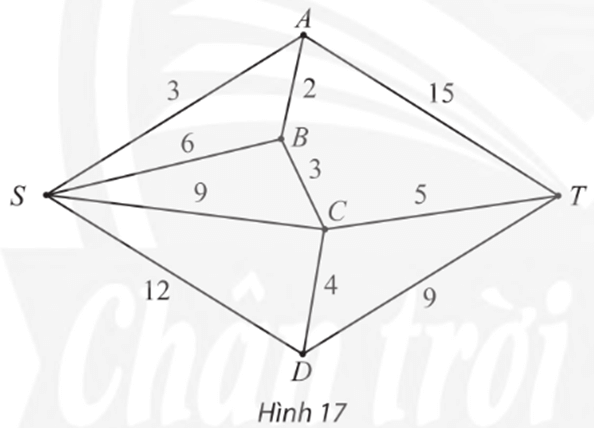
Tìm đường đi ngắn nhất từ đỉnh S đến T trong đồ thị trọng số ở Hình 17.
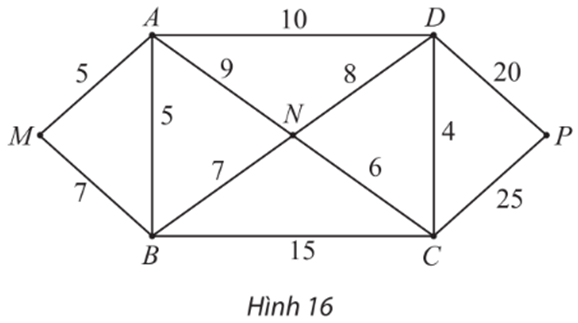
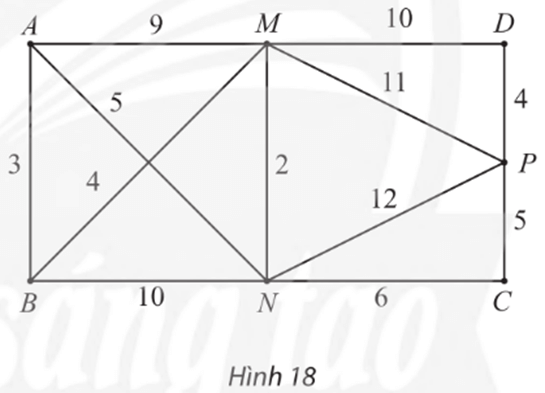
Tìm đường đi ngắn nhất từ đỉnh A đến P trong đồ thị có trọng số ở Hình 18.