Câu hỏi:
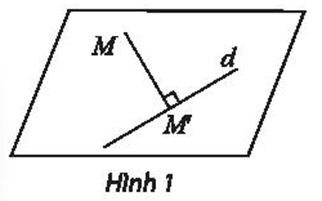
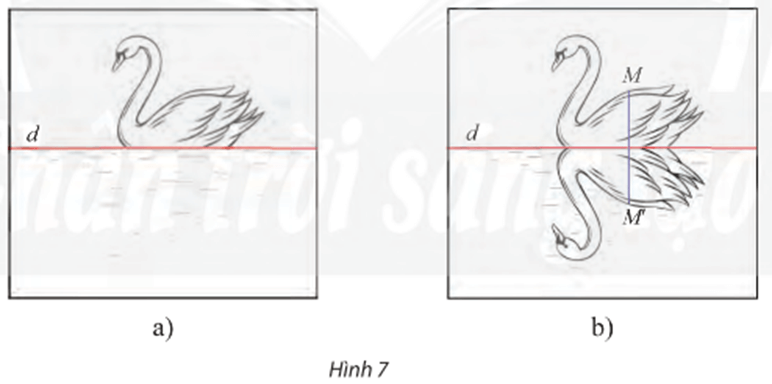
92 lượt xemCho đường thẳng d cố định, xét phép biến hình f biến điểm M thuộc d thành chính nó và biến điểm M không thuộc d thành điểm M’ sao cho d là trung trực của đoạn MM’. Hãy chứng minh f là một phép dời hình.
Lời giải
Hướng dẫn giải:
• Phép biến hình f biến 1 điểm thuộc d thành chính nó, do đó khoảng cách giữa hai điểm bất kì thuộc d qua phép biến hình f được bảo toàn (1)
• Lấy hai điểm M, N bất kì không thuộc d.
Ta có M’ = f(M) và N’ = f(N).
Gọi H, K lần lượt là trung điểm của MM’ và NN’.
Suy ra
Ta có:
⦁
(do H, K lần lượt là trung điểm của MM’, NN’)
⦁
Khi đó
(do d là đường trung trực của MM’, NN’ nên ).
Suy ra
Do đó MN = M’N’ (2)
Từ (1) và (2) suy ra phép biến hình f bảo toàn khoảng cách giữa hai điểm bất kì.
Vậy f là một phép dời hình.