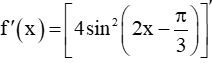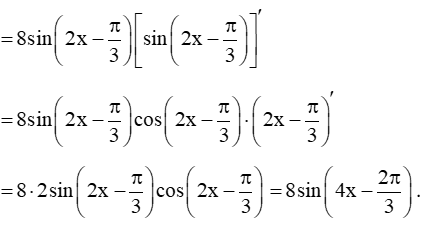Câu hỏi:
90 lượt xem Tự luận
Cho hàm số f(x) = 4sin2. Chứng minh rằng |f'(x)| ≤ 8 với mọi x ℝ. Tìm x để f'(x) = 8.
Lời giải
Hướng dẫn giải:
+ Có
Vì 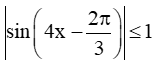
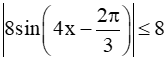
Vậy |f'(x)| ≤ 8 với mọi x ℝ.
+ Có f'(x) = 8 8sin=8
(k ℤ)
(k ℤ)
(k ℤ).
Vậy f'(x) = 8 khi với k ℤ.
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 7:
Tự luận
Biết y là hàm số của x thỏa mãn phương trình xy = 1 + lny. Tính y'(0).
1 năm trước
132 lượt xem
Câu 8: