Câu hỏi:
91 lượt xem Tự luận
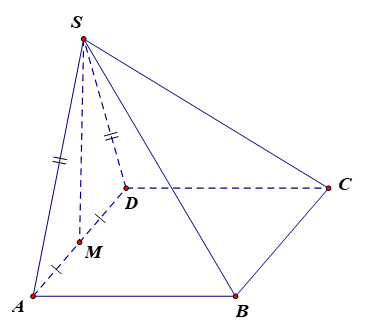
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tam giác SAD là tam giác đều và M là trung điểm của cạnh AD. Tính góc giữa hai đường thẳng BC và SA; BC và SM.
Lời giải
Hướng dẫn giải:
Vì ABCD là hình bình hành nên BC // AD. Do đó (BC, SA) = (AD, SA) = .
Do tam giác SAD đều nên = 60o .
Vậy góc giữa hai đường thẳng BC và SA bằng 60°.
Vì ABCD là hình bình hành nên BC // AD. Do đó (BC, SM) = (AD, SM).
Vì M là trung điểm của AD nên SM là đường trung tuyến.
Xét tam giác đều SAD có SM là đường trung tuyến nên SM là đường cao.
Do đó SM AD hay (AD, SM) = 90°.
Vậy góc giữa hai đường thẳng BC và SM bằng 90°.
Câu 2:
Câu 3:
Câu 4: