Câu hỏi:
40 lượt xemCho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.
Lời giải
Hướng dẫn giải:
|
GT |
ABC cân tại A, AD là phân giác của |
|
KL |
AD là đường trung trực của tam giác ABC. |
Chứng minh (Hình vẽ dưới đây):
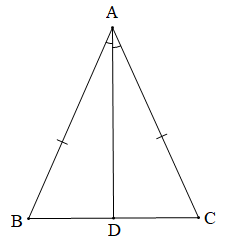
Tam giác ABC cân tại A (giả thiết) nên AB = AC.
Vì AD là đường phân giác của (giả thiết) nên (tính chất tia phân giác)
Xét ABD và ACD có:
AB = AC (chứng minh trên),
(chứng minh trên),
AD là cạnh chung.
Do đó ABD = ACD (c.g.c).
Suy ra BD = CD (hai cạnh tương ứng) và (hai góc tương ứng).
+) Vì BD = CD mà D nằm giữa B và C nên D là trung điểm của BC. (1)
+) Vì và (tính chất hai góc kề bù)
Nên .
Do đó AD BC. (2)
Từ (1) và (2) ta có AD vuông góc với BC tại trung điểm D của BC.
Vậy AD là đường trung trực của đoạn thẳng BC.
Cho tam giác ABC như Hình 122. Vẽ đường trung trực d của đoạn thẳng BC
Trong Hình 127, điểm O có phải là giao điểm ba đường trung trực của tam giác ABC không
