Câu hỏi:
81 lượt xemLời giải
Hướng dẫn giải:
a) Kẻ AH vuông góc với BC tại H.
Khi M di chuyển trên BC thì tạo ra các đường xiên AM kẻ từ A xuống BC.
Trường hợp đặc biệt khi M trùng với H thì AM là đường vuông góc.
Mà trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
Vậy M là chân đường cao kẻ từ A đến BC thì độ dài AM nhỏ nhất.
b)
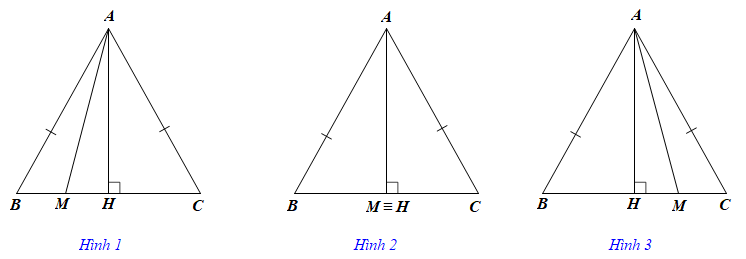
Ta xét các trường hợp sau:
• M nằm giữa B và H (Hình 1):
là góc tù nên ABM là tam giác tù.
Khi đó cạnh AB đối diện với là cạnh lớn nhất của ABM.
Hay AM < AB (1)
• M trùng với H (Hình 2):
AH, AB lần lượt là đường vuông góc và đường xiên kẻ từ A đến BC.
Khi đó AH là đường ngắn nhất nên AH = AM < AB (2)
• M nằm giữa H và C (Hình 3):
là góc tù nên AMC là tam giác tù.
Khi đó cạnh AC đối diện với là cạnh lớn nhất của AMC.
Hay AM < AC
Mà AB = AC (do ABC cân tại A).
Do đó AM < AB (3)
Từ (1), (2) và (3) ta có AM < AB.
Vậy AM < AB.
