Câu hỏi:
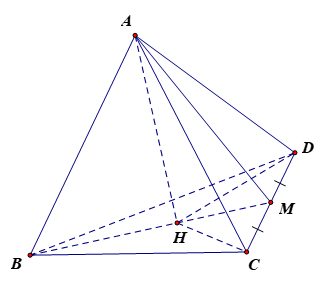
164 lượt xemCho tứ diện đều ABCD có độ dài các cạnh bằng a. Gọi M là trung điểm của CD, kẻ AH vuông góc với BM tại H.
a) Chứng minh rằng AH (BCD).
b) Tính côsin của góc giữa mặt phẳng (BCD) và mặt phẳng (ACD).
Lời giải
Hướng dẫn giải:
a) Vì M là trung điểm của CD nên BM là trung tuyến.
Vì BCD là tam giác đều nên CD BM.
Tương tự CD AM nên CD (ABM), suy ra CD ^ AH.
Mà AH BM nên AH (BCD).
b) Vì AM CD, BM CD nên góc giữa hai mặt phẳng (BCD) và mặt phẳng (ACD) bằng góc giữa hai đường thẳng AM và BM, mà (AB,BM) = .
Tam giác BCD đều có BM là đường cao đồng thời là trung tuyến, ta chứng minh được H là trọng tâm tam giác BCD nên BM = và HM = BM = .
Tam giác ADC đều có AM là đường cao đồng thời là trung tuyến nên AM = .
Xét tam giác AHM vuông tại H nên cos = cos.
Vậy côsin của góc giữa mặt phẳng (BCD) và mặt phẳng (ACD) bằng .