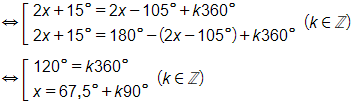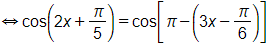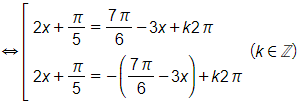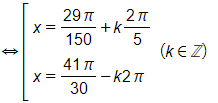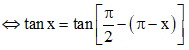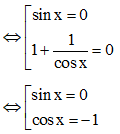Câu hỏi:
169 lượt xemGiải các phương trình sau:
a) sin(2x + 15°) + cos(2x – 15°) = 0;
b) ;
c) tan x + cot x = 0;
d) sin x + tan x = 0.
Lời giải
Hướng dẫn giải:
a) Ta có sin(2x + 15°) + cos(2x – 15°) = 0
⇔ sin(2x + 15°) = – cos(2x – 15°)
⇔ sin(2x + 15°) = – sin[90° – (2x – 15°)]
⇔ sin(2x + 15°) = sin[– 90° + (2x – 15°)]
⇔ sin(2x + 15°) = sin(2x – 105°)
Không xảy ra trường hợp 120° = k360°.
Vậy phương trình đã cho có nghiệm x = 67,5° + k90° (k ∈ ℤ).
b)
c) Ta có tan x + cot x = 0
⇔ tan x = – cot x
⇔ tan x = cot(π – x)
. Vô lí.
Vậy phương trình đã cho vô nghiệm.
d) Điều kiện cos x ≠ 0 .
Ta có sin x + tan x = 0
⇔ sin x = 0 (do sin2 x + cos2 x = 1)
⇔ x = kπ (k ∈ ℤ).
Vì x = kπ (k ∈ ℤ) thoả mãn điều kiện cos x ≠ 0 nên nghiệm của phương trình đã cho là
x = kπ (k ∈ ℤ).
Giải các phương trình sau:
a) ;
b) ;
c) 3tan 2x + = 0;
d) cot (2x – 3) = cot 15°.