Tính các giới hạn sau: 

a) $\underset{n\to +\infty }{\lim }\left(\sqrt{n^2+2n}-n-2\right)$ ;

b) $\underset{n\to +\infty }{\lim }\left(2+n^2-\sqrt{n^4+1}\right)$ ;

c) $\underset{n\to +\infty }{\lim }\left(\sqrt{n^2-n+2}+n\right)$ ;

d) $\underset{n\to +\infty }{\lim }\left(3n-\sqrt{4n^2+1}\right)$ .

Tính các giới hạn sau: 

a) $\underset{n\to +\infty }{\lim }\frac{n^2+1}{2n^2+n+2}$ ;

b) $\underset{n\to +\infty }{\lim }\frac{2^n+3}{1+3^n}$ .

Một người thợ đang cố gắng đặt tấm kính ABCD (mép AB không song song với CD) dựa vào tường sao cho mép kính CD song song với đường chân tường, còn mép AB nằm hoàn toàn trên tường. Sau một hồi loay hoay, người thợ vẫn không thể đặt được tấm kính như mong muốn. Hãy giải thích tại sao.

Có cách nào để đặt tấm kính để một mép kính song song với đường chân tường, một mép kính khác nằm hoàn toàn trên tường không?

Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’. Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng và MNPQ là hình bình hành.

Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Gọi M, N, M’, N’ lần lượt là trung điểm của các cạnh AB, CD, A’B’, C’D’.

a) Chứng minh rằng bốn điểm M, N, M’, N’ đồng phẳng và tứ giác MNN’M’ là hình bình hành

b) Giả sử MN không song song với BC. Xác định giao tuyến của hai mặt phẳng (MNN’M’) và (BCC’B’).

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi O là một điểm nằm trong tam giác SAD.

a) Xác định giao điểm của đường thẳng AO và mặt phẳng (SCD).

b) Xác định giao tuyến của hai mặt phẳng (SBO) và (SAC).

c) Xác định giao điểm của đường thẳng BO và mặt phẳng (SAC).

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) chứa đường thẳng AD và cắt hai cạnh SB, SC lần lượt tại E, F.

a) Xác định giao tuyến của hai mặt phẳng (EAB) và (FCD).

b) Chứng minh rằng tứ giác AEFD là hình thang.

c) Xác định giao tuyến của hai mặt phẳng (ECD) và (FAB).

d) Chứng minh rằng giao tuyến của hai mặt phẳng (ECD) và (FAB) song song với giao tuyến của hai mặt phẳng (EAB) và (FCD).

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là trung điểm của các cạnh AA’, AB, AC

a) Chứng minh rằng BC//(MNP).

b) Xác định giao tuyến d của hai mặt phẳng (MNP) và (A’B’C’)

c) Chứng minh rằng d//NP

Cho hình chóp ngũ giác S.ABCDE. Giả sử AB song song với DE.

a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBE).

b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SDE).

c) Giả sử giao tuyến của hai mặt phẳng (SAE) và (SBC) song song với đường thẳng AE. Chứng minh AE//BC

Cho mặt phẳng (P) và điểm A nằm ngoài mặt phẳng (P). Khẳng định nào sau đây là đúng?

A. Qua A có vô số mặt phẳng song song với (P)                   

B. Qua A có đúng một mặt phẳng song song với (P)                       

C. Qua A không có mặt phẳng song song với (P)                            

D. Qua A có đúng hai mặt phẳng song song với (P)

Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d. Khi đó

A. d là tập hợp tất cả các điểm nằm trong mặt phẳng (P) và nằm ngoài mặt phẳng Q           

B. d là tập hợp tất cả các điểm nằm ngoài mặt phẳng (P) và nằm trong mặt phẳng Q           

C. d là tập hợp tất cả các điểm nằm ngoài cả hai mặt phẳng (P) và (Q)    

D. d là tập hợp tất cả các điểm nằm trong cả hai mặt phẳng (P) và (Q)

Cho hình hộp chữ nhật ABCD.A’B’C’D’. Hình chiếu song song của điểm A trên mặt phẳng (CDD’C’) theo phương BC’ là:

A. D’                   

B. D                     

C. B                     

D. C’

Cho tứ diện ABCD có E, F lần lượt là trung điểm của các cạnh BC, CD. Mặt phẳng (P) chứa đường thẳng EF và cắt mặt phẳng (ABD) theo giao tuyến d. Khi đó

A. d song song với BC           

B. d song song với AB           

C. d song song với BD           

D. d song song với CD

Chọn hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD). Khi đó, d đi qua S và song song với

A. AC        

B. CD                  

C. BD        

D. BC

Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng d cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C. Đường thẳng d’ cắt các mặt phẳng (P), (Q), (R) lần lượt tại A’, B’, C’. Biết rằng $\frac{AB}{AC}=\frac{2}{3}$, tỉ số $\frac{A^{\prime }{B}^{\prime }}{A^{\prime }{C}^{\prime }}$ bằng

A. $\frac{1}{3}$          

B. $\frac{2}{3}$          

C. $\frac{3}{2}$          

D. $\frac{1}{2}$.

Nếu mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) lần lượt theo hai giao tuyến a và b thì vị trí tương đối giữa hai đường thẳng a và b là:

A. song song                                    

B. chéo nhau       

C. trùng nhau                                   

D. cắt nhau

Cho tứ diện ABCD. Một mặt phẳng cắt các cạnh AB, BC, CD, DA của tứ diện lần lượt tại M, N, P, Q. Khi đó

A. MN, AC, PQ đồng quy.     

B. MN, AC, PQ đôi một song song.          

C. MN, AC, PQ đôi một chéo nhau.

D. MN, AC, PQ đôi một song song hoặc chéo nhau.

Trong không gian cho hai đường thẳng cắt nhau a và b. Nếu c là một đường thẳng song song với a thì

A. c và b song song  

B. c và b cắt nhau   

C. c và b chéo nhau  

D. c và b không song song với nhau

Ba chiếc gậy được đặt dựa vào tường và đôi một song song với nhau (H.4.32). Giải thích vì sao nếu ba đầu gậy trên tường thẳng hàng thì ba đầu gậy trên sàn cũng thẳng hàng.

Trong các hình sau, hình nào là hình biểu diễn của lăng trụ tứ giác có hai đáy là hình thang?

Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình vuông.

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng cố định không song song với MN. Gọi A’, B’, C’, D’, M’, N’ lần lượt là hình chiếu của A, B, C, D, M, N qua phép chiếu lên mặt phẳng (P) theo phương MN.

a) Chứng minh rằng hai điểm M’ và N’ trùng nhau.

b) Chứng minh rằng bốn điểm A’, B’, C’, D’ là bốn đỉnh của một hình bình hành.

Cho hình chóp S.ABCD có đáy ABCD không là hình thang.

a) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)

b) Xác định hình chiếu của điểm A qua phép chiếu song song lên mặt phẳng (SCD) theo phương SB.

Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Gọi O là giao điểm của AC và BD. Gọi O’ là hình chiếu của O qua phép chiếu song song lên mặt phẳng (A’B’C’D’) theo phương AA’. Chứng minh rằng O’ là giao điểm của A’C’ và B’D’.

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M là điểm thuộc cạnh BC sao cho $MB=2MC.$

a) Xác định hình chiếu M’ của M qua phép chiếu song song lên mặt phẳng (A’B’C’) theo phương AA’.

b) Chứng minh rằng $M^{\prime }{B}^{\prime }=2M^{\prime }{C}^{\prime }$

Một chiếc bình nước hình trụ được đặt trên bàn, lượng nước trong bình bằng đúng một nửa dung tích của bình. Hoàng đặt một chiếc ống hút vào trong bình sao cho cho một đầu của ống hút chạm vào đáy bình còn một đầu chạm vào miệng bình. Hoàng nói rằng độ dài của phần ống hút bị ướt bằng độ dài của toàn bộ ống hút. Hỏi Hoàng nói đúng hay sai? Vì sao?

Khi cắt một chiếc bánh gato hình hộp, Thúy nhận thấy vết cắt ở mặt trên và mặt dưới của bánh gợi nên hình ảnh về hai đường thẳng song song với nhau. Hỏi nhận xét của Thúy có đúng không? Vì sao?

Cho hình hộp ABCD.A’B’C’D’. Gọi O là giao điểm của các đường chéo của hình hộp. Mặt phẳng qua O và song song với mặt phẳng (ABCD) cắt các cạnh AA’, BB’, CC’, DD’ lần lượt tại M, N, P, Q.

a) Chứng minh rằng M, N, P, Q lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’.

b) Chứng minh rằng ABCD.MNPQ là hình hộp.

Cho ba mặt phẳng (P), (Q), (R) đôi một song song. Hai đường thẳng d, d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’. Biết rằng AB = 2cm, BC = 6cm và A’B’ = 3cm, tính B’C’.

Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:

a) AB’//C’D’;      

b) Hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.

Cho hình hộp ABCD.A’B’C’D’.

a) Xác định giao tuyến d của hai mặt phẳng (ADC’B’) và (A’D’CB).

b) Chứng minh rằng d // AD.

c) Chứng minh rằng d đi qua trung điểm của các đường chéo của hình hộp.

Cho hình hộp ABCD.A’B’C’D’. Một mặt phẳng (P) cắt các cạnh AD, BC, B’C’, A’D’ lần lượt tại E, F, G, H. Chứng minh rằng tứ giác EFGH là hình bình hành.

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Chứng minh rằng sau điểm A, B, C, D, E, F là sáu đỉnh của một hình lăng trụ tam giác.

Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có đáy ABCD là hình thang. Chứng minh rằng đáy A’B’C’D’ là hình thang.

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E là một điểm bất kì thuộc cạnh SA và (P) là mặt phẳng qua E song song với mặt phẳng (ABCD).

a) Xác định giao tuyến của mặt phẳng (P) và các mặt bên của hình chóp.

b) Hình tạo bởi các giao tuyến là hình gì? Giải thích vì sao.

Cho tứ diện ABCD và một điểm O nằm trong tam giác BCD. Gọi (P) là mặt phẳng qua O và song song với mặt phẳng (ABD).

a) Xác định giao tuyến của mặt phẳng (P) và mặt phẳng (BCD).

b) Xác định giao tuyến của mặt phẳng (P) và các mặt còn lại của tứ diện.

Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường a, b, c, d đôi một song song và không nằm trong mặt phẳng (ABCD).

a) Chứng minh rằng hai mặt phẳng mp(a,b) và mp(c,d) song song với nhau.

b) Chứng minh rằng hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau.

c) Một mặt phẳng cắt bốn đường thẳng a, b, c, d lần lượt tại A’, B’, C’, D’. Chứng minh rằng tứ giác A’B’C’D’ là hình bình hành.

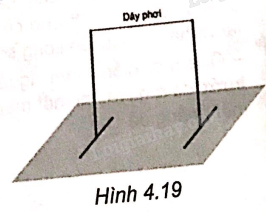
Để dựng dây phơi quần áo, bác Việt lắp hai thanh sắt đứng có chiều dài bằng nhau trên mặt đất và căng dây nối hai đầu còn lại của hai thanh sắt (H.4.19). Khi đó, dây phơi có song song với mặt đất không? Giải thích vì sao.

Một tấm bảng hình chữ nhật được đặt dựa vào tường như trong Hình 4.18. Hãy giải thích vì sao mép trên của tấm bảng song song với mặt đất, mép dưới của tấm bảng song song với mặt tường.

Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Gọi E là một điểm bất kì thuộc cạnh SA. Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng AB và SC.

a) Xác định giao tuyến của mặt phẳng (P) và mặt phẳng (SAC), từ đó tìm một điểm chung của mặt phẳng (P) và mặt phẳng (ABCD).

b) Xác định giao tuyến của mặt phẳng (P) và mặt phẳng (ABCD).

c) Xác định giao tuyến của mặt phẳng (P) và các mặt còn lại của hình chóp.