Câu hỏi:
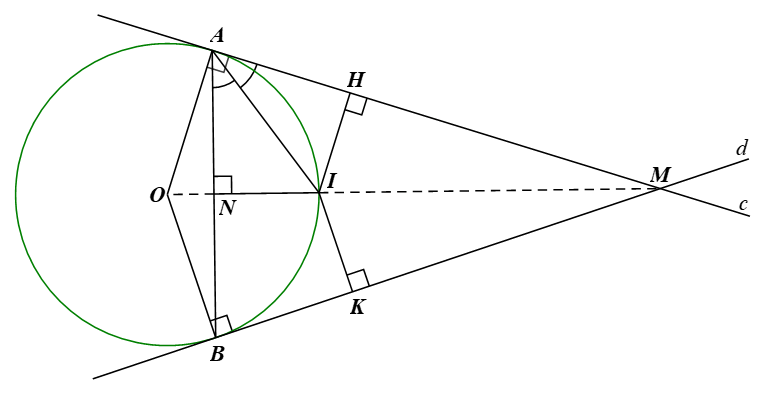
65 lượt xemCho đường tròn (O) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d đi qua M lần lượt tiếp xúc với (O) tại A, B. Tia phân giác của góc MAB cắt MO tại I. Chứng minh điểm I cách đều ba đường thẳng MA, MB và AB.
Lời giải
Hướng dẫn giải:
Gọi H, K và N lần lượt là hình chiếu của I lên MA, MA và AB.
Theo cách vẽ, ta có IH ⊥ MA, IK ⊥ MB, IN ⊥ AB nên ˆIHA=ˆIHM=ˆIKM=ˆANI=90°.
Xét ∆ANI (vuông tại N) và ∆AHI (vuông tại H) có:
AI là cạnh chung; ˆNAI=ˆHAI (do AI là phân giác của ˆMAB).
Do đó ∆ANI = ∆AHI (cạnh huyền – góc nhọn).
Suy ra IN = IH (hai cạnh tương ứng). (1)
Vì MA, MB là hai tiếp tuyến của đường tròn (O) cắt nhau tại M với A, B là các tiếp điểm nên MO là tia phân giác của ˆAMB hay MI là tia phân giác của ˆHMK.
Xét ∆MHI (vuông tại H) và ∆MKI (vuông tại K) có:
MI là cạnh chung và ˆHMI=ˆKMI (do MI là tia phân giác của ˆHMK).
Do đó ∆MHI = ∆MKI (cạnh huyền – góc nhọn).
Suy ra IH = IK (hai cạnh tương ứng). (2)
Từ (1) và (2) suy ra IN = IH = IK.
Vậy điểm I cách đều ba đường thẳng MA, MB và AB.
ĐỀ THI LIÊN QUAN:
-
13 câu hỏi 83 lượt thi -
21 câu hỏi 80 lượt thi