Câu hỏi:
118 lượt xem Tự luận
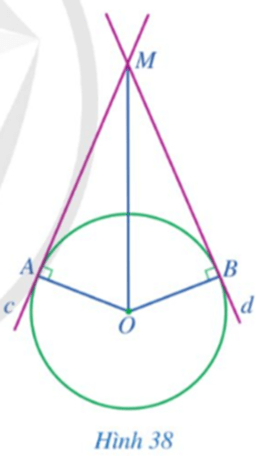
Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d qua M lần lượt tiếp xúc với (O) tại A, B. Biết ˆAMB=120°. Chứng minh AB = R.
Lời giải
Hướng dẫn giải:
Vì MA, MB là hai tiếp tuyến của đường tròn (O; R) nên OA = OB = R và OA ⊥ AM tại A, OB ⊥ BM tại B hay ˆOAM=90°;ˆOBM=90°.
Xét tứ giác OAMB có: ˆAOB+ˆOAM+ˆOBM+ˆAMB=360°(định lí tổng các góc của một tứ giác).
Suy ra ˆAOB=360°−(ˆOAM+ˆOBM+ˆAMB)
Nên ˆAOB=360°−(90°+90°+120°)=60°.
Xét tam giác OAB có OA = OB = R và ˆAOB=60° nên là tam giác đều.
Do đó AB = OA = OB = R.
Vậy AB = R.
Câu 1:
Câu 3:
Câu 5:
Câu 6:
Câu 10:
Câu 11: