Câu hỏi:
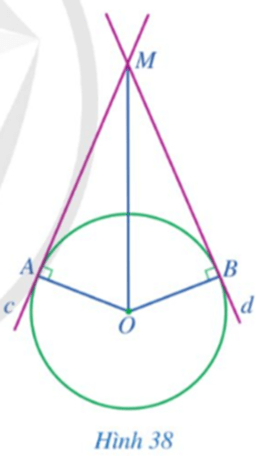
65 lượt xemCho đường tròn (O; R). Các đường thẳng c, d lần lượt tiếp xúc với đường tròn (O; R) tại A, B và cắt nhau tại M (Hình 38).
a) Các tam giác MOA và MOB có bằng nhau hay không?
b) Hai đoạn thẳng MA và MB có bằng nhau hay không?
c) Tia MO có phải là tia phân giác của góc AMB hay không?
d) Tia OM có phải tia phân giác của góc AOB hay không?
Lời giải
Hướng dẫn giải:
a) Xét ∆MOA (vuông tại A) và ∆MOB (vuông tại B) có:
OA = OB = R (A, B cùng thuộc đường tròn (O; R));
OM là cạnh chung.
Do đó ∆MOA = ∆MOB (cạnh huyền – cạnh góc vuông).
b) Vì ∆MOA = ∆MOB (câu a) nên MA = MB (hai cạnh tương ứng).
c) Vì ∆MOA = ∆MOB (câu a) nên ˆOMA=ˆOMB (hai góc tương ứng)
Do đó MO là phân giác của ˆAMB.
d) Vì ∆MOA = ∆MOB (câu a) nên ˆMOA=ˆMOB (hai góc tương ứng)
Do đó OM là phân giác của ˆAOB