Câu hỏi:
61 lượt xem Tự luận
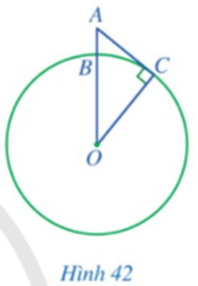
Cho ba điểm A, B, C thẳng hàng, trong đó B nằm giữa A và C. Đường tròn (O) tiếp xúc với đường thẳng AB tại điểm C. Chứng minh AO2 + BC2 = BO2 + AC2.
Lời giải
Hướng dẫn giải:
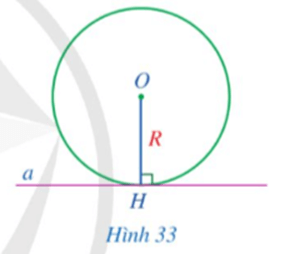
Vì đường tròn (O) tiếp xúc với đường thẳng AB tại điểm C nên OC ⊥ AC tại C.
Xét ∆OAC vuông tại C, ta có: AO2 = AC2 + CO2 (định lí Pythagore).
Suy ra CO2 = AO2 – AC2.
Xét ∆OBC vuông tại C, ta có: BO2 = BC2 + CO2 (định lí Pythagore).
Suy ra CO2 = BO2 – BC2.
Do đó AO2 – AC2 = BO2 – BC2
Hay AO2 + BC2 = BO2 + AC2.
Câu 1:
Câu 5:
Câu 6:
Câu 8:
Câu 10:
Câu 11: