Câu hỏi:
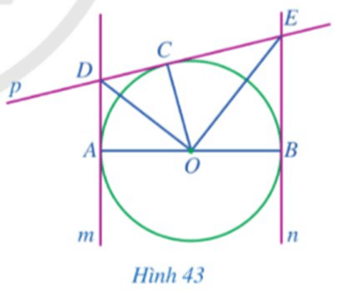
73 lượt xemCho đường tròn (O; R) đường kính AB và các đường thẳng m, n, p lần lượt tiếp xúc với đường tròn tại A, B, C (Hình 43).
Chứng minh:
a) AD + BE = DE;
b) ˆCOD=12ˆCOA và ˆCOE=12ˆCOB.
c) Tam giác ODE vuông.
d) OD⋅OEDE=R.
Lời giải
Hướng dẫn giải:
a) Vì DA, DC là hai tiếp tuyến của đường tròn (O) cắt nhau tại D nên DA = DC (tính chất hai tiếp tuyến cắt nhau).
Vì EB, EC là hai tiếp tuyến của đường tròn (O) cắt nhau tại E nên EB = EC (tính chất hai tiếp tuyến cắt nhau).
Do đó DA + EB = DC + EC hay AD + BE = DE.
b) Vì DA, DC là hai tiếp tuyến của đường tròn (O) cắt nhau tại D nên OA là tia phân giác của ˆCOA (tính chất hai tiếp tuyến cắt nhau).
Do đó ˆCOD=12ˆCOA=12 (tính chất tia phân giác).
Vì EB, EC là hai tiếp tuyến của đường tròn (O) cắt nhau tại E nên OE tia phân giác của ˆCOB (tính chất hai tiếp tuyến cắt nhau).
Do đó ˆCOE=12ˆCOB=12 (tính chất tia phân giác).
c) Ta có: ˆDOE=ˆCOD+ˆCOE
Mà ˆCOD=12ˆCOA=12 và ˆCOE=12ˆCOB=12 (chứng minh ở câu b)
Do đó ˆDOE=12(ˆCOA+ˆCOB)=12ˆAOB=12⋅180°=90°.
Vậy tam giác ODE vuông tại O.
d) Vì DE là tiếp tuyến của đường tròn (O) tại C nên OC ⊥ DE tại C.
Xét ∆ODE và ∆CDO có:
ˆDOE=ˆDCO=90° và ˆODE là góc chung
Do đó ∆ODE ᔕ ∆CDO (g.g)
Suy ra OECO=DEDO (tỉ số các cạnh tương ứng)
Nên CO = OD⋅OEDE hay OD⋅OEDE= R.