Câu hỏi:
26 lượt xemCho ∆ABC đều có cạnh bằng 2. Qua ba phép biến hình liên tiếp: Phép tịnh tiến , phép quay Q(B, 60°), phép vị tự V(A, 3), ∆ABC biến thành ∆A1B1C1. Tìm diện tích ∆A1B1C1.
Lời giải
Hướng dẫn giải:
Ta có ∆ABC đều có cạnh bằng 2. Suy ra AB = AC = 2 và .
Vì phép tịnh tiến và phép quay đều là phép dời hình nên ảnh của ∆ABC qua phép tịnh tiến và phép quay Q(B, 60°) đều có các kích thước bằng các kích thước tương ứng của ∆ABC.
Gọi f là phép biến hình có được bằng thực hiện hai phép biến hình liên tiếp là phép tịnh tiến và phép quay Q(B, 60°).
Suy ra f là phép dời hình.
Do đó phép đồng dạng tỉ số 3 có được bằng cách thực hiện liên tiếp phép dời hình f và phép vị tự V(A, 3) biến ∆ABC thành ∆A1B1C1.
Vì vậy phép đồng dạng tỉ số 3 biến các điểm A, B, C theo thứ tự thành các điểm A1, B1, C1.
Khi đó A1B1 = 3AB = 3.2 = 6 và A1C1 = 3AC = 3.2 = 6.
Vì ∆ABC và ∆A1B1C1 đồng dạng với nhau nên .
Ta có .
Vậy diện tích ∆A1B1C1 bằng .
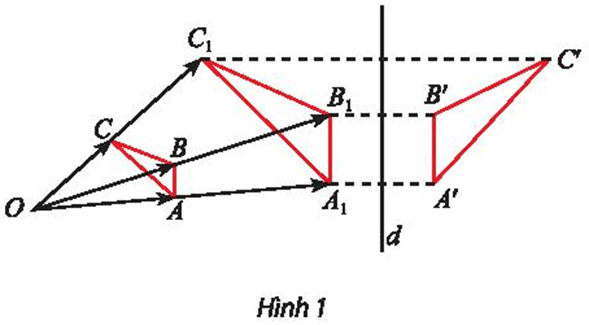
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.


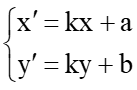 . Hãy chứng minh g là một phép đồng dạng.
. Hãy chứng minh g là một phép đồng dạng.