Câu hỏi:
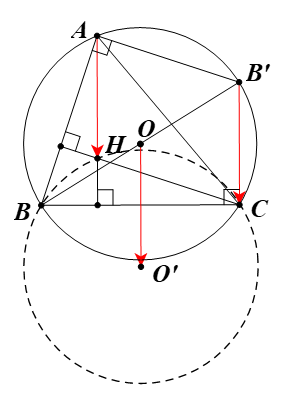
83 lượt xemCho hai điểm B, C cố định trên đường tròn (O; R) và một điểm A thay đổi trên đường tròn đó. Chứng minh trực tâm H của tam giác ABC luôn nằm trên một đường tròn cố định.
Lời giải
Hướng dẫn giải:
Kẻ đường kính BB’.
Do B, C cố định trên (O) nên B’, C cũng cố định trên (O).
Suy ra là vectơ không đổi.
Ta có (góc nội tiếp chắn nửa đường tròn (O)).
Suy ra BC ⊥ B’C.
Mà AH ⊥ BC (do H là trực tâm của ∆ABC).
Do đó AH // B’C (1)
Chứng minh tương tự, ta được AB’ // CH (2)
Từ (1), (2), suy ra tứ giác AHCB’ là hình bình hành.
Suy ra AH = B’C.
Mà AH // B’C (chứng minh trên).
Vì vậy .
Do đó .
Vậy khi A thay đổi trên đường tròn (O) thì trực tâm H của tam giác ABC luôn nằm trên ảnh của đường tròn (O) là đường tròn (O’) qua .
Phép dời hình nào có thể biến hình ngôi sao A thành hình ngôi sao B?