Câu hỏi:
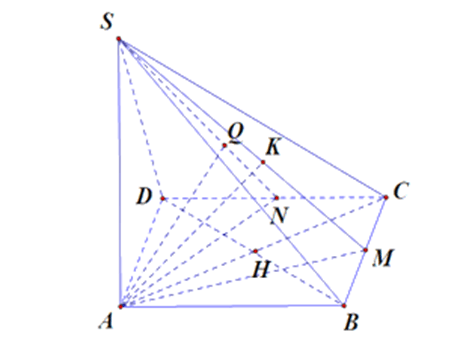
181 lượt xemCho hình chóp S.ABC có đáy là tam giác ABC đều cạnh bằng a, SA (ABC) và SA = 2a. Tính theo a khoảng cách:
a) Từ điểm B đến mặt phẳng (SAC).
b) Từ điểm A đến mặt phẳng (SBC).
c) Giữa hai đường thẳng AB và SC.
Lời giải
Hướng dẫn giải:
a) Kẻ BH AC tại H.
Vì SA (ABC) nên SA BH mà BH AC. Suy ra, BH (SAC).
Vì ABC là tam giác đều cạnh a có BH là đường cao nên BH = .
Do đó d(B, (SAC)) = BH = .
b) Kẻ AM BC tại M, AK SM tại K
Do SA (ABC) nên SA BC mà AM BC nên BC (SAM), suy ra BC AK.
Vì AK SM và BC AK thì AK (SBC).
Suy ra d(A, (SBC)) = AK.
Tam giác ABC đều cạnh bằng a có AM là đường cao nên AM = .
Vì SA (ABC) nên SA AM.
Xét tam giác SAM vuông tại A, có AK = 2a. Vậy d(A, (SBC)) = 2a.
c) Dựng hình bình hành ABCD thì AB // CD nên AB // (SCD) và mặt phẳng (SCD) chứa SC nên d(AB, SC) = d(AB, (SCD)). Mà d(AB, (SCD)) = d(A, (SCD)).
Kẻ AN DC tại N, kẻ AQ SN tại Q
Vì ADC là tam giác đều, AN là đường cao nên AN = .
Vì SA (ABC) nên SA (ABCD), suy ra SA DC mà AN DC nên DC (SAN).
Vì DC (SAN) nên DC AQ mà AQ SN nên AQ (SDC).
Khi đó d(A, (SCD)) = AQ.
Xét tam giác SAN vuông tại A, có . Vậy d(AB, SC) = .