Câu hỏi:
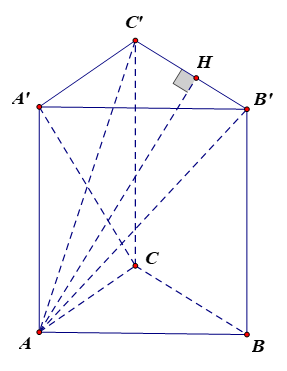
295 lượt xemCho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A và AB = AC = AA' = a. Tính theo a khoảng cách:
a) Từ điểm A đến đường thẳng B'C'.
b) Giữa hai đường thẳng BC và AB'.
Lời giải
Hướng dẫn giải:
a) Hạ AH B'C' tại H. Khi đó d(A, B'C') = AH.
Vì ABC.A'B'C' là lăng trụ đứng nên các mặt bên là hình chữ nhật, do đó AA' = BB' = CC' = a, AB = A'B' = a; AC = A'C' = a, BC = B'C'.
Xét tam giác ABB' vuông tại B, có AB' = .
Xét tam giác ACA' vuông tại A, có A'C = .
Suy ra AC' = a.
Xét tam giác ABC vuông tại A, có BC = .
Suy ra B'C' = a.
Do đó AB' = AC' = B'C' = a. Suy ra tam giác AB'C' đều.
Xét tam giác AB'C' đều có AH là đường cao nên AH = .
Vậy d(A, B'C') = .
b) Do BCC'B' là hình chữ nhật nên BC // B'C'.
Suy ra BC // (AB'C') nên d(BC, AB') = d(BC, (AB'C')) = d(C, (AB'C')).
Do ACC'A' là hình chữ nhật nên CA' cắt AC' tại trung điểm của CA' do đó
d(C, (AB'C')) = d(A', (AB'C')).
Đặt d(A', (AB'C')) = h. Áp dụng kết quả bài 7.7 trang 28 SBT Toán 11 tập 2, ta có:
.
Vậy d(BC, AB') = .