Câu hỏi:
47 lượt xem Tự luận
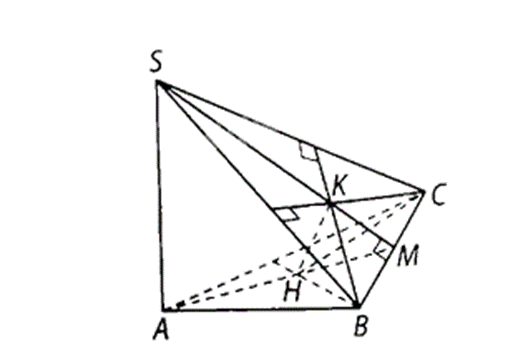
Cho hình chóp S.ABC có SA (ABC), tam giác ABC nhọn. Gọi H, K lần lượt là trực tâm của tam giác ABC và SBC. Chứng minh rằng:
a) BC (SAH) và các đường thẳng AH, BC, SK đồng quy;
b) SB (CHK) và HK (SBC).
Lời giải
Hướng dẫn giải:
a) Vì H là trực tâm tam giác ABC nên BC AH,
mà SA (ABC) nên SA BC. Do đó BC (SAH).
Gọi M là giao điểm của AH và BC, ta có BC (SAM) nên BC SM.
Mặt khác, K là trực tâm của tam giác SBC nên SM đi qua K.
Do đó AH, BC, SK đồng quy.
b) Vì SA (ABC) nên SA CH, mà CH AB, suy ra CH (SAB).
Do đó CH SB.
Lại có SB CK nên SB (CHK).
Xét tam giác SBC, K là trực tâm nên BK SC.
Vì SA (ABC) nên SA BH mà BH CA nên BH (SAC), suy ra BH SC.
Vì BK SC và BH SC nên SC (BHK), suy ra SC HK.
Mà SB HK (vì SB (CHK)). Do đó HK (SBC).
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
