Câu hỏi:
73 lượt xem Tự luận
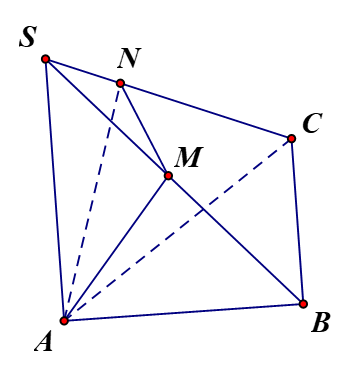
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy là tam giác ABC vuông tại B. Kẻ AM vuông góc với SB tại M và AN vuông góc với SC tại N. Chứng minh rằng:
a) BC (SAB);
b) AM (SBC);
c) SC (AMN).
Lời giải
Hướng dẫn giải:
a) Vì SA (ABC) nên SA BC mà AB BC (do tam giác ABC vuông tại B). Do đó BC (SAB).
b) Vì BC (SAB) nên BC AM, mà AM SB (giả thiết). Do đó AM (SBC).
c) Vì AM (SBC) nên AM SC, mà AN SC (giả thiết). Do đó SC (AMN).
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6: