Câu hỏi:
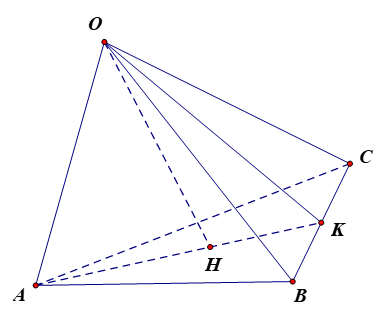
133 lượt xemCho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi H là chân đường vuông góc hạ từ O đến mặt phẳng (ABC). Chứng minh rằng:
a) BC (OAH);
b) H là trực tâm của tam giác ABC;
c) .
Lời giải
Hướng dẫn giải:
a) Vì OA OB, OA OC nên OA (OBC). Suy ra OA BC.
Mà OH (ABC) nên OH BC. Do đó BC (OAH).
b) Vì BC (OAH) nên BC AH, do đó AH là đường cao của tam giác ABC. (1)
Có OH (ABC) nên OH AC.
Có OB OA, OC OB nên OB (OAC) nên OB AC mà OH AC, từ đó suy ra AC (OBH), suy ra CA BH, do đó BH là đường cao của tam giác ABC. (2)
Từ (1) và (2) suy ra H là giao hai đường cao của tam giác ABC.
Do đó H là trực tâm của tam giác ABC.
c) Gọi K là giao điểm của AH với BC.
Vì OA (OBC) nên OA OK .
Xét tam giác OAK vuông tại O, có OH là đường cao nên .
Vì AK BC mà OA BC nên BC (OAK), suy ra OK BC.
Xét tam giác OBC vuông tại O, có OK là đường cao nên .
Do đó .