Câu hỏi:
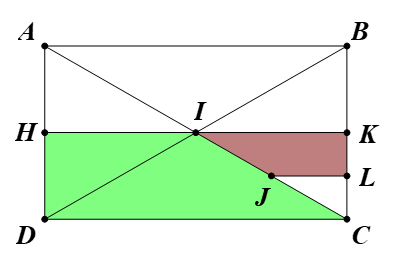
81 lượt xemCho hình chữ nhật ABCD có AC cắt BD tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hình thang JLKI và hình thang IHDC đồng dạng với nhau.
Lời giải
Hướng dẫn giải:
Ta có J là trung điểm IC (giả thiết).
Suy ra .
Do đó V(C, 2)(J) = I.
Chứng minh tương tự, ta được V(C, 2)(L) = K, V(C, 2)(K) = B, V(C, 2)(I) = A.
Vì vậy V(C, 2) biến hình thang JLKI thành hình thang IKBA.
Hình chữ nhật ABCD có I là giao điểm của hai đường chéo, suy ra I là trung điểm BD.
Do đó ĐI(B) = D.
Chứng minh tương tự, ta được ĐI(A) = C, ĐI(K) = H.
Lại có ĐI(I) = I.
Do đó ĐI biến hình thang IKBA thành hình thang IHDC.
Vì vậy phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm C, tỉ số 2 và phép đối xứng tâm I biến hình thang JLKI thành hình thang IHDC.
Vậy hình thang JLKI và hình thang IHDC đồng dạng với nhau.
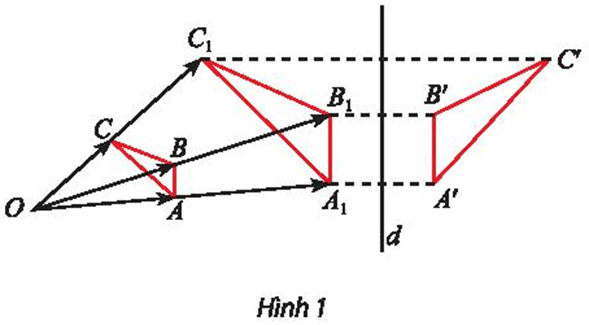
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.

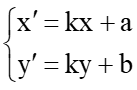 . Hãy chứng minh g là một phép đồng dạng.
. Hãy chứng minh g là một phép đồng dạng.