Câu hỏi:
141 lượt xemCho tam giác ABC có = 120°. Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.
Lời giải
Hướng dẫn giải:
|
GT |
ABC, AD là tia phân giác góc A DE // AB |
|
KL |
ADE đều. |
Chứng minh (Hình vẽ dưới đây)
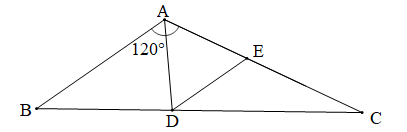
Vì AD là tia phân giác góc A (giả thiết)
Nên (tính chất tia phân giác của một góc)
Mà nên
Lại có DE // AB (giả thiết) nên (hai góc so le trong)
Do đó tam giác ADE có
Suy ra tam giác ADE là tam giác cân có một góc bằng 60°.
Suy ra tam giác ADE là tam giác đều.
Vậy tam giác ADE là tam giác đều.
Trong Hình 68, hai cạnh AB và AC của tam giác ABC có bằng nhau hay không?
