Câu hỏi:
94 lượt xemCho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân
Lời giải
Hướng dẫn giải:
|
GT |
ABC vuông cân tại A M là trung điểm của cạnh huyền BC |
|
KL |
MAB vuông cân. |
Chứng minh (Hình vẽ dưới đây)
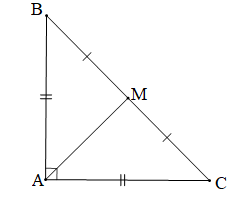
+) Tam giác ABC là tam giác vuông cân tại A (giả thiết) nên AB = AC và
Xét tam giác ABM và tam giác ACM có:
AM là cạnh chung
MB = MC (M là trung điểm của BC)
AB = AC (chứng minh trên)
Do đó ABM = ACM (c.c.c)
Suy ra (hai góc tương ứng)
Nên tia AM là tia phân giác của góc A
Do đó
+) Xét tam giác MAB có
Do đó tam giác MAB cân tại M. (1)
Lại có (hai góc tương ứng của ABM = ACM)
Mà (tính chất hai góc kề bù)
Do đó
Nên tam giác MAB vuông tại M. (2)
Từ (1) và (2) suy ra tam giác MAB vuông cân tại M.
Trong Hình 68, hai cạnh AB và AC của tam giác ABC có bằng nhau hay không?
