Giải Toán 11 Bài 2: Công thức lượng giác

Bài giảng Toán 11 Bài 2: Công thức lượng giác

Giải Toán 11 trang 17 Tập 1

Mở đầu trang 17 Toán 11 Tập 1: Một thiết bị trễ kĩ thuật số lặp lại tín hiệu đầu vào bằng cách lặp lại tín hiệu đó trong một khoảng thời gian cố định sau khi nhận được tín hiệu. Nếu một thiết bị như vậy nhận được nốt thuần f1(t) = 5sin t và phát lại được nốt thuần f2(t) = 5cos t thì âm kết hợp là f(t) = f1(t) + f2(t), trong đó t là biến thời gian. Chứng tỏ rằng âm kết hợp viết được dưới dạng f(t) = ksin (t + φ), tức là âm kết hợp là một sóng âm hình sin. Hãy xác định biên độ âm k và pha ban đầu φ (– π ≤ φ ≤ π) của sóng âm.

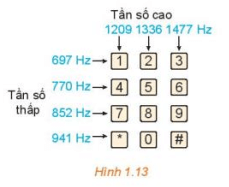
Vận dụng 1 trang 18 Toán 11 Tập 1: Giải bài toán trong tình huống mở đầu.

HĐ2 trang 18 Toán 11 Tập 1: Xây dựng công thức nhân đôi

Lấy b = a trong các công thức cộng, hãy tìm công thức tính: sin 2a; cos 2a; tan 2a.

Giải Toán 11 trang 19 Tập 1

Luyện tập 2 trang 19 Toán 11 Tập 1: Không dùng máy tính, tính $\cos \frac{\pi }{8}$.

HĐ3 trang 19 Toán 11 Tập 1: Xây dựng công thức biến đổi tích thành tổng

a) Từ các công thức cộng cos(a + b) và cos(a – b), hãy tìm: cos a cos b; sin a sin b.

b) Từ các công thức cộng sin(a + b) và sin(a – b), hãy tìm: sin a cos b.

Luyện tập 3 trang 19 Toán 11 Tập 1: Không dùng máy tính, tính giá trị của các biểu thức:

A = cos 75° cos 15°; B = $\sin \frac{5\pi }{12}\cos \frac{7\pi }{12}$.

Giải Toán 11 trang 20 Tập 1

HĐ4 trang 20 Toán 11 Tập 1: Xây dựng công thức biến đổi tổng thành tích

Trong các công thức biến đổi tích thành tổng ở Mục 3, đặt u = a – b, v = a + b và viết các công thức nhận được.

Luyện tập 4 trang 20 Toán 11 Tập 1: Không dùng máy tính, tính giá trị của biểu thức

$B = \cos \frac{\pi }{9}+\cos \frac{5\pi }{9}+\cos \frac{11\pi }{9} .$

Vận dụng 2 trang 20 Toán 11 Tập 1: Khi nhấn một phím trên điện thoại cảm ứng, bàn phím sẽ tạo ra hai âm thuần, kết hợp với nhau để tạo ra âm thanh nhận dạng duy nhất phím. Hình 1.13 cho thấy tần số thấp f1 và tần số cao f2 liên quan đến mỗi phím. Nhấn một phím sẽ tạo ra sóng âm y = sin(2πf1t) + sin(2πf2t), ở đó t là biến thời gian (tính bằng giây).

a) Tìm hàm số mô hình hóa âm thanh được tạo ra khi nhấn phím 4.

b) Biến đổi công thức vừa tìm được ở câu a về dạng tích của một hàm số sin và một hàm số côsin.

Giải Toán 11 trang 21 Tập 1

Bài tập

Bài 1.7 trang 21 Toán 11 Tập 1: Sử dụng 15° = 45° – 30°, hãy tính các giá trị lượng giác của góc 15°.

Bài 1.8 trang 21 Toán 11 Tập 1: Tính:

a) $\cos \left(a+\frac{\pi }{6}\right)$, biết $\sin a=\frac{1}{\sqrt{3}}$ và $\frac{\pi }{2}<a<\pi$;

b) $\tan \left(a-\frac{\pi }{4}\right)$, biết $\cos a=-\frac{1}{3}$ và $\pi <a<\frac{3\pi }{2}$.

Bài 1.9 trang 21 Toán 11 Tập 1: Tính sin 2a, cos 2a, tan 2a, biết:

a) $\sin a=\frac{1}{3}$ và $\frac{\pi }{2}<a<\pi$;

b) sin a + cos a = $\frac{1}{2}$ và $\frac{\pi }{2}<a<\frac{3\pi }{4}$.

Bài 1.10 trang 21 Toán 11 Tập 1: Tính giá trị của các biểu thức sau:

a) $A=\frac{\sin \frac{\pi }{15}\cos \frac{\pi }{10}+\sin \frac{\pi }{10}\cos \frac{\pi }{15}}{\cos \frac{2\pi }{15}\cos \frac{\pi }{5}-\sin \frac{2\pi }{15}\sin \frac{\pi }{5}}$;

b) $B=\sin \frac{\pi }{32}\cos \frac{\pi }{32}\cos \frac{\pi }{16}\cos \frac{\pi }{8}$.

Bài 1.11 trang 21 Toán 11 Tập 1: Chứng minh đẳng thức sau:

sin(a + b) sin(a – b) = sin2 a – sin2 b = cos2 b – cos2 a.

Bài 1.12 trang 21 Toán 11 Tập 1: Cho tam giác ABC có $\widehat{B}=75°$; $\widehat{C}=45°$ và a = BC = 12 cm.

a) Sử dụng công thức $S=\frac{1}{2}ab\sin C$ và định lí sin, hãy chứng minh diện tích của tam giác ABC cho bởi công thức

$S=\frac{a^2\sin B\sin C}{2\sin A}$.

b) Sử dụng kết quả ở câu a và công thức biến đổi tích thành tổng, hãy tính diện tích S của tam giác ABC.

Bài 1.13 trang 21 Toán 11 Tập 1: Trong Vật lí, phương trình tổng quát của một vật dao động điều hòa cho bởi công thức x(t) = Acos(ωt + φ), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời điểm t, A là biên độ dao động (A > 0) và φ ∈ [–π; π] là pha ban đầu của dao động.

Xét hai dao động điều hòa có phương trình:

$x_1\left(t\right)=2\cos \left(\frac{\pi }{3}t+\frac{\pi }{6}\right)$ (cm),

$x_2\left(t\right)=2\cos \left(\frac{\pi }{3}t-\frac{\pi }{3}\right)$ (cm).

Tìm dao động tổng hợp x(t) = x1(t) + x2(t) và sử dụng công thức biến đổi tổng thành tích để tìm biên độ và pha ban đầu của dao động tổng hợp này.