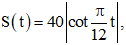Câu hỏi:
225 lượt xemMột con lắc lò xo dao động điều hoà quanh vị trí cân bằng theo phương trình y = 25 sin 4πt ở đó y được tính bằng centimét còn thời gian t được tính bằng giây.
a) Tìm chu kì dao động của con lắc lò xo.
b) Tìm tần số dao động của con lắc, tức là số lần dao động trong một giây.
c) Tìm khoảng cách giữa điểm cao nhất và thấp nhất của con lắc.
Lời giải
Hướng dẫn giải:
a) Hàm số y = 25 sin 4πt tuần hoàn với chu kì T = .
Suy ra chu kì dao động của con lắc lò xo (tức là khoảng thời gian để con lắc thực hiện được một dao động toàn phần) là T = giây.
b) Vì chu kì dao động của con lắc là T = giây nên trong 1 giây con lắc thực hiện được 2 dao động, tức là tần số dao động của con lắc là = 2 Hz.
c) Vì phương trình dao động của con lắc là y = 25 sin 4πt nên biên độ dao động của nó là A = 25 cm. Từ đó suy ra, khoảng cách giữa điểm cao nhất và điểm thấp nhất của con lắc là 2A = 50 cm.
Xét tính chẵn lẻ của các hàm số sau:
a) ;
b) y = x – sin 3x;
c) ;
d) .
![Từ đồ thị hàm số y = sin x hãy xác định các giá trị của x trên đoạn [-3π/2 ; 5π/2 ] sao cho](https://vietjack.com/sbt-toan-11-kn/images/bai-1-22-trang-18-sbt-toan-lop-11-tap-1.PNG) sao cho:
sao cho: