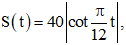Câu hỏi:
117 lượt xemXét tính tuần hoàn của các hàm số sau:
a) y = A sin(ωx + φ) với A > 0;
b) y = A tan(ωx + φ) với A > 0;
c) y = 3 sin 2x + 3cos 2x;
d) .
Lời giải
Hướng dẫn giải:
a) Tập xác định của hàm số là D = ℝ.
Nếu kí hiệu f(x) = A sin(ωx + φ) thì với mọi x ∈ D, ta có
và
= A sin(ωx + 2π + φ) = A sin(ωx + φ) = f(x).
Vậy hàm số đã cho là hàm số tuần hoàn, chu kì của hàm số này là .
b) Nếu kí hiệu D là tập xác định của hàm số f(x) = A tan(ωx + φ) thì với mọi x ∈ D, ta có:
và
= A tan(ωx + π + φ) = A tan(ωx + φ) = f(x).
Vậy hàm số đã cho là hàm số tuần hoàn, chu kì của hàm số này là .
c) Ta có 3sin 2x + 3cos 2x = 3(sin 2x + cos 2x) = .
Theo câu a, ta suy ra hàm số y = 3sin 2x + 3cos 2x là hàm số tuần hoàn chu kì .
d) Ta có
.
Vậy theo câu a, hàm số là hàm số tuần hoàn chu kì .
Xét tính chẵn lẻ của các hàm số sau:
a) ;
b) y = x – sin 3x;
c) ;
d) .
![Từ đồ thị hàm số y = sin x hãy xác định các giá trị của x trên đoạn [-3π/2 ; 5π/2 ] sao cho](https://vietjack.com/sbt-toan-11-kn/images/bai-1-22-trang-18-sbt-toan-lop-11-tap-1.PNG) sao cho:
sao cho: