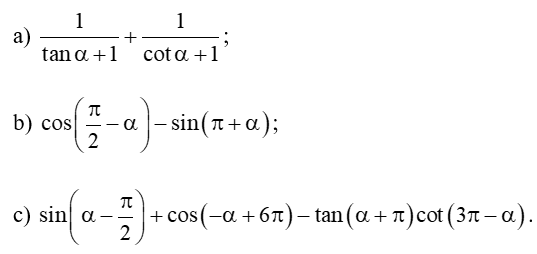3. Các xác định một mặt phẳng
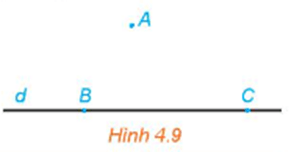
HĐ6 trang 74 Toán 11 Tập 1: Cho đường thẳng d và điểm A không thuộc d. Trên đường thẳng d lấy hai điểm B, C phân biệt (H.4.9). Mặt phẳng (ABC) có chứa điểm A và đường thẳng d hay không? Mặt phẳng (ABC) có chứa hai đường thẳng AB và BC hay không?
Bài 10: Đường thẳng và mặt phẳng trong không gian
HĐ3 trang 72 Toán 11 Tập 1: Trong Hình 4.4 là một khối rubik có bốn đỉnh và bốn mặt, mỗi mặt là một tam giác.
a) Đặt khối rubik sao cho ba đỉnh của mặt màu đỏ đều nằm trên mặt bàn. Khi đó, mặt màu đỏ của khối rubik có nằm trên mặt bàn hay không?
b) Có thể đặt khối rubik sao cho 4 đỉnh của nó đều nằm trên mặt bàn hay không?
Bài 10: Đường thẳng và mặt phẳng trong không gian
2. Các tính chất thừa nhận
Giải Toán 11 trang 72
HĐ2 trang 72 Toán 11 Tập 1: Chiếc xà ngang đặt tựa lên hai điểm A, B của trụ nhảy thể hiện hình ảnh của một đường thẳng đi qua hai điểm đó. Có thể tìm được một đường thẳng khác cũng đi qua hai điểm A, B này không?
Bài 10: Đường thẳng và mặt phẳng trong không gian
Giải Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian
Bài giảng Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian
1. Khái niệm mở đầu
Giải Toán 11 trang 71
Câu hỏi trang 71 Toán 11 Tập 1: Hãy tìm một số hình ảnh của mặt phẳng trong thực tế.
Bài 10: Đường thẳng và mặt phẳng trong không gian
Bài 3.15 trang 69 Toán 11 Tập 1: Một bảng xếp hạng đã tính điểm chuẩn hóa cho chỉ số nghiên cứu của một số trường đại học ở Việt Nam và thu được kết quả sau:
|
Điểm |
Dưới 20 |
[20; 30) |
[30; 40) |
[40; 60) |
[60; 80) |
[80; 100) |
|
Số trường |
4 |
19 |
6 |
2 |
3 |
1 |
Xác định điểm ngưỡng để đưa ra danh sách 25% trường đại học có chỉ số nghiên cứu tốt nhất Việt Nam.
Bài tập cuối chương 3
B. Tự luận
Bài 3.13 trang 69 Toán 11 Tập 1: Cơ cấu dân số Việt Nam năm 2020 theo độ tuổi được cho trong bảng sau:
|
Độ tuổi |
Dưới 5 tuổi |
5 – 14 |
15 – 24 |
25 – 64 |
Trên 65 |
|
Số người (triệu) |
7,89 |
14,68 |
13,32 |
53,78 |
7,66 |
(Theo: http:ourwworldindata.org)
Chọn 80 là giá trị đại diện cho nhóm trên 65 tuổi. Tính tuổi trung bình của người Việt Nam năm 2020.
Bài tập cuối chương 3
Giải Toán 11 Bài tập cuối chương 3
Bài giảng Toán 11 Bài tập cuối chương 3
A. Trắc nghiệm
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
|
Thời gian (phút) |
[0; 20) |
[20; 40) |
[40; 60) |
[60; 80) |
[80; 100) |
|
Số học sinh |
5 |
9 |
12 |
10 |
6 |
Bảng 3.6
Giải Toán 11 trang 69
Bài 3.8 trang 69 Toán 11 Tập 1: Giá trị đại diện của nhóm [20; 40) là
A. 10.
B. 20.
C. 30.
D. 40.
Bài tập cuối chương 3
Bài 8 trang 20 Toán 11 Tập 1: Khi đạp xe di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển , khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58 cm? Giả sử độ dàu của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.
Giải Toán 11 (Chân trời sáng tạo) Bài 2: Giá trị lượng giác của một góc lượng giác
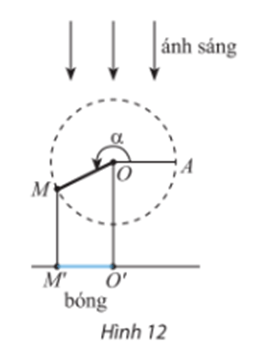
Bài 7 trang 20 Toán 11 Tập 1: Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được vòng là bao nhiêu, biết độ dài thanh OM là 15 cm? Kết quả làm tròn đến hàng phần mười.
Giải Toán 11 (Chân trời sáng tạo) Bài 2: Giá trị lượng giác của một góc lượng giác
Vận dụng trang 19 Toán 11 Tập 1:
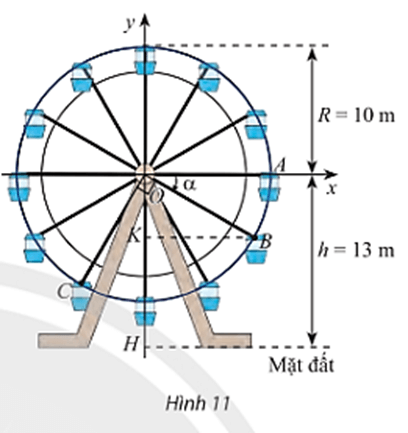
Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu bởi điểm B và C.
a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng (13 + 10sinα) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi α = – 30°.
b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.
Giải Toán 11 (Chân trời sáng tạo) Bài 2: Giá trị lượng giác của một góc lượng giác
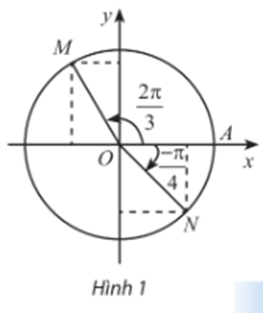
Hoạt động khám phá 3 trang 17 Toán 11 Tập 1: Cho . Biểu diễn các góc lượng giác – α, α + π, π – α, trên đường tròn lượng giác và rút ra mối liên hệ giữa giá trị lượng giác của các góc này với giá trị lượng giác của góc α.
Giải Toán 11 (Chân trời sáng tạo) Bài 2: Giá trị lượng giác của một góc lượng giác
Hoạt động khám phá 2 trang 16 Toán 11 Tập 1: a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao sin2α + cos2α = 1.
b) Chia cả hai vễ của biểu thức ở câu a) cho cos2α ta được đẳng thức nào?
c) Chia cả hai vế của biểu thức ở câu a) cho sin2α ta được đẳng thức nào?
Giải Toán 11 (Chân trời sáng tạo) Bài 2: Giá trị lượng giác của một góc lượng giác
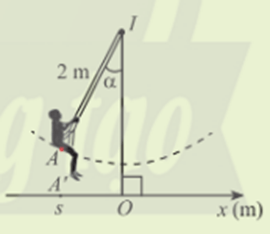
Hoạt động khởi động trang 13 Toán 11 Tập 1: Hình bên biểu diễn xích đu IA có độ dài 2m dao động quanh trục IO vuông góc với trục Ox trên mặt đất và A’ là hình chiếu của A lên Ox. Tọa độ s của A’ trên trục Ox được gọi là li độ của A và (IO, IA) = α được gọi là li độ góc của A. Làm cách nào để tính li độ dựa vào li độ góc?
Giải Toán 11 (Chân trời sáng tạo) Bài 2: Giá trị lượng giác của một góc lượng giác
Bài 3.7 trang 67 Toán 11 Tập 1: Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu ở bên.
|
Thời gian |
Số học sinh nam |
Số học sinh nữ |
|
[4; 5) |
6 |
4 |
|
[5; 6) |
10 |
8 |
|
[6; 7) |
13 |
10 |
|
[7; 8) |
9 |
11 |
|
[8; 9) |
7 |
8 |
a) So sánh thời gian ngủ trung bình của các bạn học sinh nam và nữ.
b) Hãy cho biết 75% học sinh khối 11 ngủ ít nhất bao nhiêu giờ?
Bài 9: Các số đặc trưng đo xu thế trung tâm