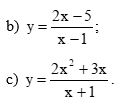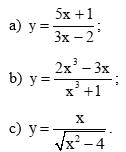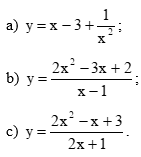Câu hỏi:
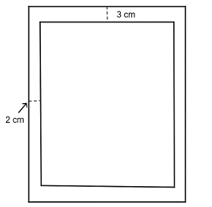
83 lượt xemMột trang sách có dạng hình chữ nhật với diện tích là 384 cm2. Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất?
Lời giải
Hướng dẫn giải:
Gọi x (cm) là chiều rộng của trang sách.
Khi đó, chiều dài của trang sách là (cm).
Sau khi để lề thì phần in chữ có dạng hình chữ nhật có chiều rộng là x – 4 (cm) và chiều dài là - 6 (cm).
Rõ ràng, x phải thỏa mãn điều kiện 4 < x < 64.
Diện tích phần in chữ trên trang sách là
S(x) = (x - 4)= (cm2).
Xét hàm số S(x) = với x ∈ (4; 64).
Ta có S'(x) = < 0;
S'(x) = 0 ⇔ – 6x2 + 1 536 = 0 ⇔ x = – 16 hoặc x = 16.
Khi đó trên khoảng (4; 64), S'(x) = 0 khi x = 16.
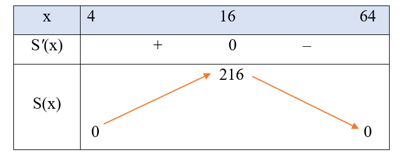
Bảng biến thiên của hàm số S(x) như sau:
Căn cứ vào bảng biến thiên, ta thấy: Trên khoảng (4; 64), hàm số S(x) đạt giá trị lớn nhất bằng 216 tại x = 16. Khi đó, .
Vậy kích thước tối ưu của trang sách là 16 × 24 (cm) thì in chữ trên trang sách có diện tích lớn nhất.
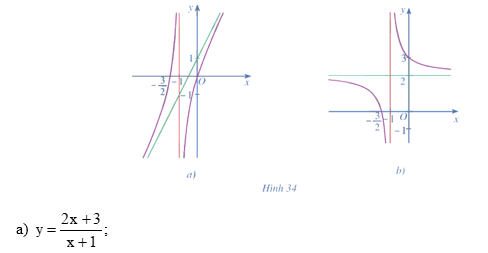
Tìm các đường tiệm cận ngang và tiệm cận đứng của đồ thị mỗi hàm số sau:
Tìm các đường tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau: