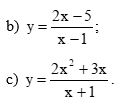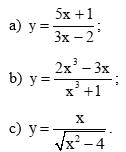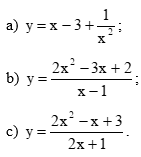Câu hỏi:
75 lượt xemTìm giá trị nhỏ nhất và giá trị lớn nhất của mỗi hàm số sau:
a) f(x) = 2x3 – 6x trên đoạn [– 1; 3];
b) f(x) = trên đoạn [1; 5];
c) trên đoạn [0; 3];
d) f(x) = 2sin 3x + 7x + 1 trên đoạn .
Lời giải
Hướng dẫn giải:
a) Ta có f'(x) = 6x2 – 6. Khi đó trên khoảng (– 1; 3), f'(x) = 0 khi x = 1.
f(– 1) = 4, f(1) = – 4, f(3) = 36.
Vậy f(x) = 36 tại x = 3, f(x) = -4 tại x = 1.
b) Ta có f'(x) = . Khi đó trên khoảng (1; 5), không tồn tại x để f'(x) = 0.
f(1) = , f(5) = .
Vậy f(x) = tại x = 5, f(x) = tại x = 1.
c) Ta có f'(x) = . Khi đó trên khoảng (0; 3), f'(x) = 0 khi x = e – 1.
f(0) = 0, f(e – 1) = , f(3) = .
Vậy f(x) = tại x = 3, f(x) = 0 tại x = 0.
d) Ta có f'(x) = 6cos 3x + 7. Khi đó trên khoảng , ta có f'(x) > 0.
,
Vậy f(x) = tại x = , f(x) = 3 - tại x = -.
Tìm các đường tiệm cận ngang và tiệm cận đứng của đồ thị mỗi hàm số sau:
Tìm các đường tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau: