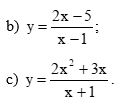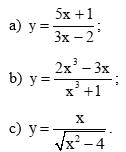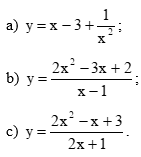Câu hỏi:
118 lượt xemKhảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
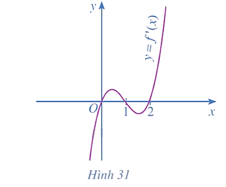
a) y = x3 – 3x2 + 2;
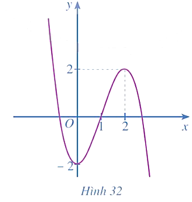
b) y = – x3 + 3x2 – 6x;
c) ;
d) ;
e) ;
g) .
Lời giải
Hướng dẫn giải:
a) y = x3 – 3x2 + 2
1) Tập xác định: ℝ.
2) Sự biến thiên:
● Giới hạn tại vô cực: y = + , y = - .
● y' = 3x2 – 6x;
y' = 0 ⇔ 3x2 – 6x = 0 ⇔ x = 0 hoặc x = 2.
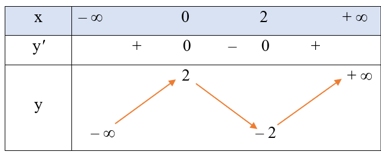
● Bảng biến thiên:
Hàm số đã cho đồng biến trên mỗi khoảng (– ∞; 0) và (2; + ∞); nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0, yCĐ = 2; đạt cực tiểu tại x = 2, yCT = – 2.
3) Đồ thị
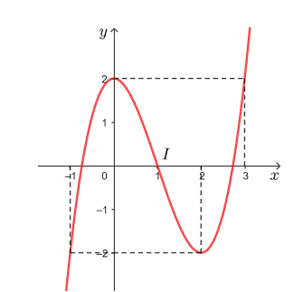
● Giao điểm của đồ thị với trục tung: (0; 2).
● Giao điểm của đồ thị với trục hoành:
Giải phương trình x3 – 3x2 + 2 = 0, ta được x = 1, x = , x = 1 + .
Vậy đồ thị hàm số cắt trục hoành tại các điểm (1; 0), (; 0), (1 + ; 0).
● Đồ thị hàm số đi qua các điểm (– 1; – 2), (0; 2), (1; 0), (2; – 2) và (3; 2).
Vậy đồ thị hàm số y = x3 – 3x2 + 2 được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là điểm I(1; 0).
b) y = – x3 + 3x2 – 6x
1) Tập xác định: ℝ.
2) Sự biến thiên:
● Giới hạn tại vô cực: y = – ∞, y = + ∞.
● y' = – 3x2 + 6x – 6 = – 3(x2 – 2x + 1) – 3 = – 3(x – 1)2 – 3 < 0 với mọi x ∈ ℝ;
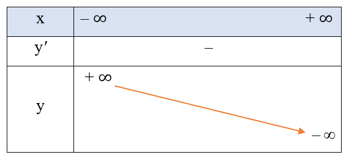
● Bảng biến thiên:
Hàm số nghịch biến trên khoảng (– ∞; + ∞).
Hàm số không có cực trị.
3) Đồ thị
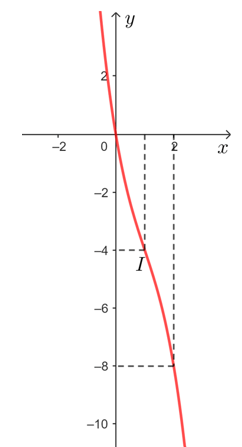
● Đồ thị hàm số đi qua gốc tọa độ O(0; 0).
● Đồ thị hàm số đi qua các điểm (0; 0), (1; – 4), (2; – 8).
Vậy đồ thị hàm số y = – x3 + 3x2 – 6x được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là gốc tọa độ I(1; – 4).
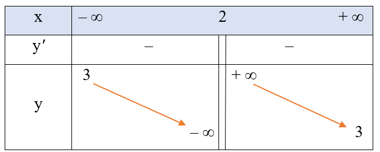
c)
1) Tập xác định: ℝ \ {2}.
2) Sự biến thiên
● Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
y = – ∞, y = + ∞ . Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
y = 3, y = 3. Do đó, đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số.
● < 0, với mọi x ≠ 2.
● Bảng biến thiên:
Hàm số nghịch biến trên mỗi khoảng (– ∞; 2) và (2; + ∞).
Hàm số không có cực trị.
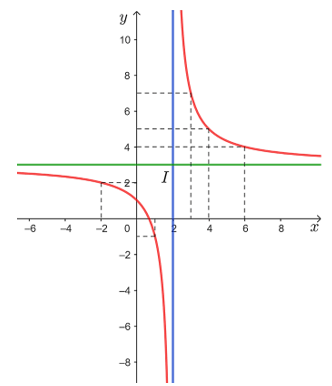
3) Đồ thị
● Giao điểm của đồ thị với trục tung: (0; 1).
● Giao điểm của đồ thị với trục hoành: .
● Đồ thị hàm số đi qua các điểm (– 2; 2), (0; 1), , (1; – 1), (3; 7), (4; 5) và (6; 4).
● Đồ thị hàm số nhận giao điểm I(2; 3) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Vậy đồ thị hàm số được cho ở hình trên.
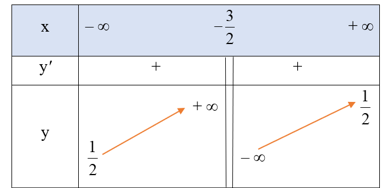
d)
1) Tập xác định: ℝ \ .
2) Sự biến thiên
● Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
y = + ∞; y = - ∞. Do đó, đường thẳng x = là tiệm cận đứng của đồ thị hàm số.
y = , y = . Do đó, đường thẳng y = là tiệm cận ngang của đồ thị hàm số.
● > 0, với mọi x ≠ .
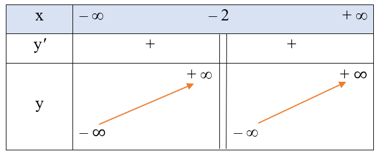
● Bảng biến thiên:
Hàm số đồng biến trên mỗi khoảng và .
Hàm số không có cực trị.
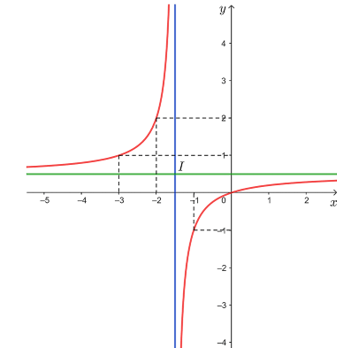
3) Đồ thị
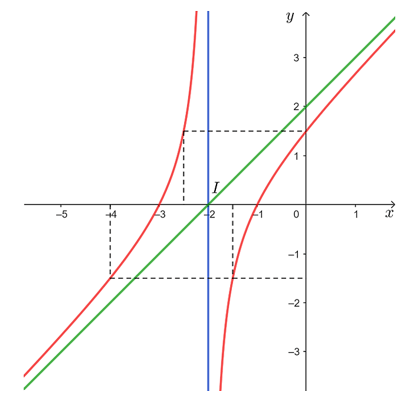
● Đồ thị hàm số đi qua gốc tọa độ O(0; 0).
● Đồ thị hàm số đi qua các điểm (– 3; 1), (– 2; 2), (– 1; – 1) và (0; 0).
● Đồ thị hàm số nhận giao điểm I của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Vậy đồ thị hàm số được cho ở hình trên.
e)
1) Tập xác định: ℝ \ {0}.
2) Sự biến thiên
● Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
Ta viết hàm số đã cho dưới dạng: .
y = + ∞, y = - ∞.
y = – ∞, y = + ∞. Do đó, đường thẳng x = 0 (hay trục Oy) là tiệm cận đứng của đồ thị hàm số.
[y - (x + 2)] = = 0, [y - (x + 2)] = = 0.
Do đó, đường thẳng y = x + 2 là tiệm cận xiên của đồ thị hàm số.
● ;
y' = 0 ⇔ x2 – 4 = 0 ⇔ x = – 2 hoặc x = 2.
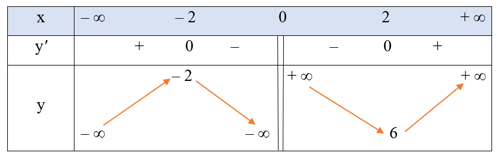
● Bảng biến thiên:
Hàm số đồng biến trên mỗi khoảng (– ∞; – 2) và (2; + ∞); nghịch biến trên mỗi khoảng (– 2; 0) và (0; 2).
Hàm số đạt cực đại tại x = – 2, yCĐ = – 2; đạt cực tiểu tại x = 2, yCT = 6.
3) Đồ thị
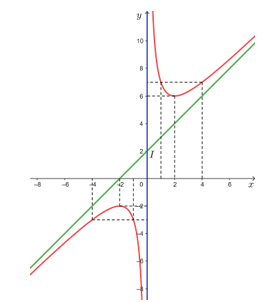
● Đồ thị hàm số không cắt các trục tọa độ.
● Đồ thị hàm số đi qua các điểm (– 4; – 3), (– 2; – 2), (– 1; – 3), (1; 7), (2; 6) và (4; 7).
● Đồ thị hàm số nhận giao điểm I(0; 2) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Vậy đồ thị hàm số được cho ở hình trên.
g)
1) Tập xác định: ℝ \ {– 2}.
2) Sự biến thiên
● Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
Ta viết hàm số đã cho dưới dạng: .
y = + ∞, y = - ∞.
y = + ∞, y = - ∞. Do đó, đường thẳng x = – 2 là tiệm cận đứng của đồ thị hàm số.
[y - (x + 2)] = = 0.; [y - (x + 2)] = = 0 Do đó, đường thẳng y = x + 2 là tiệm cận xiên của đồ thị hàm số.
●> 0 với mọi x ≠ – 2.
● Bảng biến thiên:
Hàm số đồng biến trên mỗi khoảng (– ∞; – 2) và (– 2; + ∞).
Hàm số không có cực trị.
3) Đồ thị
● Giao điểm của đồ thị với trục tung: .
● Giao điểm của đồ thị với trục hoành:
Giải phương trình ta được x = – 3, x = – 1.
Vậy đồ thị cắt trục hoành tại các điểm (– 3; 0) và (– 1; 0).
● Đồ thị hàm số đi qua các điểm , (– 3; 0), ,, (– 1; 0) và .
● Đồ thị hàm số nhận giao điểm I(– 2; 0) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Vậy đồ thị hàm số được cho ở hình trên.
Tìm các đường tiệm cận ngang và tiệm cận đứng của đồ thị mỗi hàm số sau:
Tìm các đường tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau: