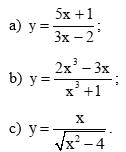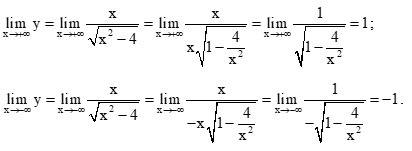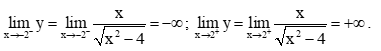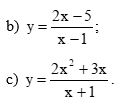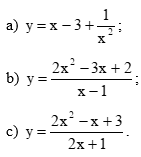Câu hỏi:
78 lượt xemLời giải
Hướng dẫn giải:
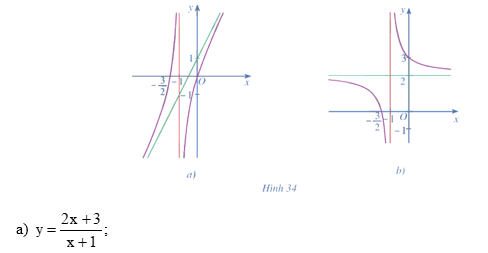
a)
Tập xác định của hàm số là .
Ta có y = = = ; y = = . Do đó, đường thẳng là tiệm cận ngang của đồ thị hàm số.
y == -; y == +. Do đó, đường thẳng là tiệm cận đứng của đồ thị hàm số.
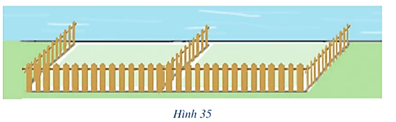
b)
Tập xác định của hàm số là ℝ \{– 1}.
Ta có y === 2; y == 2. Do đó đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
y = = + ;y = = - . Do đó, đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số.
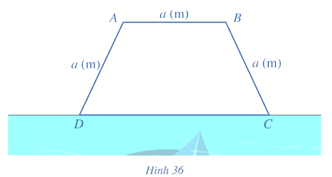
c)
Tập xác định của hàm số là (– ∞; – 2) ∪ (2; + ∞).
Ta có
Do đó, các đường thẳng y = 1 và y = – 1 là các tiệm cận ngang của đồ thị hàm số.
Ta có
Do đó, các đường thẳng x = – 2 và x = 2 là các tiệm cận đứng của đồ thị hàm số.
Tìm các đường tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau: