Câu hỏi:
126 lượt xem Tự luận
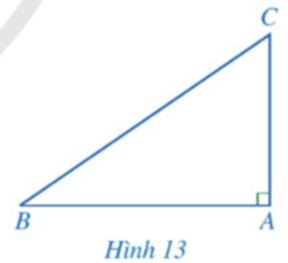
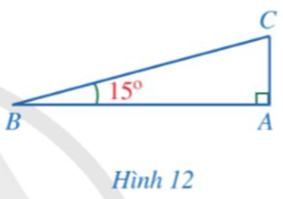
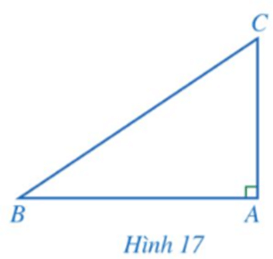
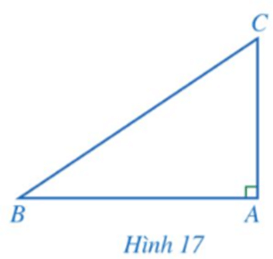
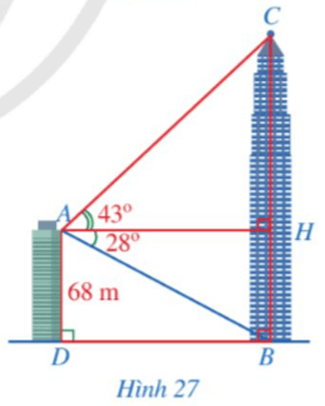
Cho tam giác ABC có đường cao AH = 6 cm, Tính độ dài các đoạn thẳng AB, BH, AC, BC (làm tròn kết quả đến hàng phần mười của centimét).
Lời giải
Hướng dẫn giải:
Xét ∆ABH vuông tại H, ta có:
⦁ sinB = , suy ra AB = = 9,3 (cm).
⦁ BH = AH.cotB = 6.cot40° ≈ 7,2 (cm).
Xét ∆ACH vuông tại H, ta có:
⦁ sinC = suy ra AC = 10,5 (cm).
⦁ CH = AH.cotC = 6.cot35° ≈ 8,6 (cm).
Khi đó, BC = BH + HC ≈ 7,2 + 8,6 = 15,8 (cm).
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Tự luận
Cho hình chữ nhật ABCD thoả mãn AC = 6 cm, Tính độ dài các đoạn thẳng AB, AD.
1 năm trước
180 lượt xem
Câu 10:
Câu 12:
Câu 13:
Câu 14:
Câu 15:
Câu 16: