Câu hỏi:
332 lượt xem Tự luận
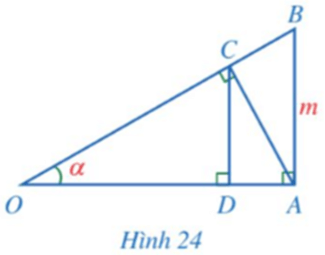
Trong Hình 24, cho , AB = m và
Chứng minh:
a) OA = m.cotα;
b) AC = m.cosα;
c) CD = m.cos2α.
Lời giải
Hướng dẫn giải:
a) Xét ∆OAB vuông tại A, ta có: OA = AB.cotO = m.cotα.
b) Xét ∆OAC vuông tại C, ta có:
AC = OA.sinO = m.cot.sin = m..sin = mcos.
(Theo kết quả câu b, Bài 7, SGK Toán 9, Tập 1, trang 81 ta có cot = ).
c) Xét ∆OAC vuông tại C, ta có:
OC = OA.cosO = m.cot.cos = m..cos = m..
(Theo kết quả câu b, Bài 7, SGK Toán 9, Tập 1, trang 81 ta có cot = )
Xét ∆OCD vuông tại D, ta có:
CD = OC.sinO = m..sin = mcos2.
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Tự luận
Cho hình chữ nhật ABCD thoả mãn AC = 6 cm, Tính độ dài các đoạn thẳng AB, AD.
1 năm trước
180 lượt xem
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 15:
Câu 16: