Câu hỏi:
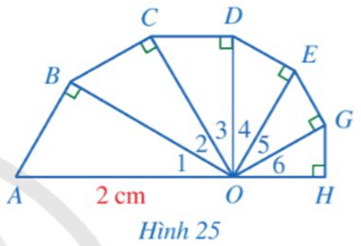
186 lượt xemTính độ dài đường gấp khúc ABCDEGH (làm tròn kết quả đến hàng phần mười của centimét), biết các tam giác OAB, OBC, OCD, ODE, OEG, OGH là các tam giác vuông tại các đỉnh lần lượt là B, C, D, E, G, H; các góc O1, O2, O3, O4, O5, O6 đều bằng 30° và OA = 2 cm (Hình 25).
Lời giải
Hướng dẫn giải:
Xét ∆OAB vuông tại B, có theo Bài 3, SGK Toám 9, Tập 1, trang 86, ta có: AB = AO = .2 = 1 (cm).
Ta cũng có BO = AO.cos = 2.cos30o = 2. = (cm).
Tương tự, ta cũng có:
⦁ BC = BO = . = (cm) và CO = BO.cos = . = (cm).
⦁ CD = CO = . = (cm) và DO = CO.cos = . = (cm).
⦁ DE = DO = . = (cm) và EO = DO.cos = . = (cm).
⦁ EG = EO = . = (cm) và GO = EO.cos = . = (cm).
⦁ GH = GO = . = (cm).
Vậy độ dài đường gấp khúc ABCDEGH là:
Cho hình chữ nhật ABCD thoả mãn AC = 6 cm, Tính độ dài các đoạn thẳng AB, AD.