Bài 3.3 trang 37 Toán 10 Tập 1

Câu hỏi:

91 lượt xem

Tự luận

Bài 3.3 trang 37 Toán 10 Tập 1: Chứng minh các hệ thức sau:

a) sin2 α + cos2 α = 1;

b) $1 + \tan^{2} α = \frac{1}{\cos^{2} α}$ (α ≠ 90o);

c) 2 $1 + \cot^{2} α = \frac{1}{\sin^{2} α}$ (0o < α < 180o).

Xem đáp án

Xem thêm: Giải Toán 10 (Kết nối tri thức) Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Lời giải

Hướng dẫn giải:

Lời giải:

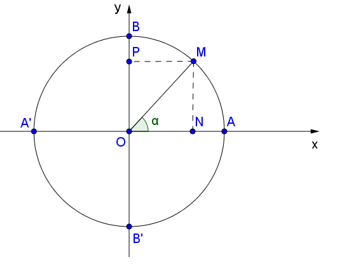
Chứng minh các hệ thức sau: sin^2 α + cos^2 α = 1 (ảnh 1)

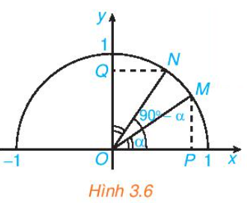
Gọi M(x; y) là điểm trên đường tròn đơn vị sao cho $\hat{x O M} = α$ .

Ta có: OM = 1 (bán kính đường tròn đơn vị).

Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Ta có: $\{\begin{cases} x = \cos α \\ y = \sin α \end{cases} \Rightarrow \{\begin{cases} x^{2} = \cos^{2} α \\ y^{2} = \sin^{2} α \end{cases}$ (1)

Mà $\{\begin{cases} |x| = O N \\ |y| = O P = M N \end{cases} \Rightarrow \{\begin{cases} x^{2} = {|x|}^{2} = O N^{2} \\ y^{2} = {|y|}^{2} = M N^{2} \end{cases}$ (2)

Từ (1) và (2) suy ra: sin2 α + cos2 α = ON2 + MN2 = OM2 = 1 (do ∆OMN vuông tại N).

Do đó sin2 α + cos2 α = 1 (đpcm).

b) Ta có: $\tan α = \frac{\sin α}{\cos α}$ (α ≠ 90o)

$1 + \tan^{2} α = 1 + \frac{\sin^{2} α}{\cos^{2} α}$

$= \frac{\cos^{2} α}{\cos^{2} α} + \frac{\sin^{2} α}{\cos^{2} α} = \frac{\cos^{2} α + \sin^{2} α}{\cos^{2} α}$ .

Mà theo câu a) ta có: sin2 α + cos2 α = 1 với mọi góc α.

$1 + \tan^{2} α = \frac{1}{\cos^{2} α}$ (đpcm)

c) Ta có: $\cot α = \frac{\cos α}{\sin α}$ (0o < α < 180o)

$1 + \cot^{2} α = 1 + \frac{\cos^{2} α}{\sin^{2} α}$

$= \frac{\sin^{2} α}{\sin^{2} α} + \frac{\cos^{2} α}{\sin^{2} α} = \frac{\sin^{2} α + \cos^{2} α}{\sin^{2} α}$ .

Mà theo câu a) ta có: sin2 α + cos2 α = 1 với mọi góc α.

$1 + \cot^{2} α = \frac{1}{\sin^{2} α}$ (đpcm).

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tự luận

Giải bài tập Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Bài giảng Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Mở đầu

Mở đầu trang 33 Toán 10 Tập 1: Bạn đã biết tỉ số lượng giác của 1 góc nhọn. Đối với góc tù thì sao?

Xem đáp án »

9 tháng trước 81 lượt xem

Câu 2:

Tự luận

1. Gía trị lượng giác của 1 góc

Giải Toán 10 trang 34 Tập 1

HĐ 1 trang 34 Toán 10 Tập 1:

a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:

• α = 90o;

• α < 90o;

• α > 90o.

b) Khi 0o < α < 90o, nêu mối quan hệ giữa cos α, sin α với hoành độ và tung độ của điểm M.

Xem đáp án »

9 tháng trước 77 lượt xem

Câu 3:

Tự luận

Giải Toán 10 trang 35 Tập 1

Luyện tập 1 trang 35 Toán 10 Tập 1: Tìm các giá trị lượng giác của góc 120o (H.3.4).

Xem đáp án »

9 tháng trước 84 lượt xem

Câu 4:

Tự luận

2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Giải Toán 10 trang 36 Tập 1

HĐ 2 trang 36 Toán 10 Tập 1: Nêu nhận xét về vị trí của hai điểm M và M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa sin α và sin (180o – α), giữa cos α và cos (180o – α).

Xem đáp án »

9 tháng trước 97 lượt xem

Câu 5:

Tự luận

Luyện tập 2 trang 36 Toán 10 Tập 1: Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau α và 90o – α $(\hat{x O M} = α, \hat{x O N} = 90^{o} - α)$ . Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa cos α và sin (90o – α).

Xem đáp án »

9 tháng trước 58 lượt xem

Câu 6:

Tự luận

Giải Toán 10 trang 37 Tập 1

Vận dụng trang 37 Toán 10 Tập 1: Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay người đó ở độ cao bao nhiêu mét?