Câu hỏi:
97 lượt xemLời giải
Hướng dẫn giải:
a) y = 3 +
1. Tập xác định: D = ℝ\{0}.
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm y' = . Vì y' < 0 với mọi x ≠ 0 nên hàm số đã cho nghịch biến trên mỗi khoảng (– ∞; 0) và (0; + ∞).
● Tiệm cận:
Ta có . Suy ra đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số.
Ta có . Suy ra đường thẳng x = 0 (hay trục Oy) là tiệm cận đứng của đồ thị hàm số.
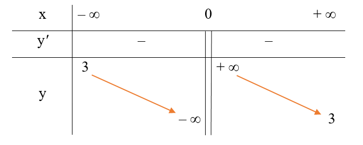
● Bảng biến thiên:
3. Đồ thị:
Ta có y = 0 ⇔ 3 + = 0 nên đồ thị hàm số cắt trục Ox tại điểm .
Đồ thị hàm số không cắt trục Oy.
Ngoài ra, đồ thị hàm số đi qua các điểm (– 1; 2) và (1; 4).
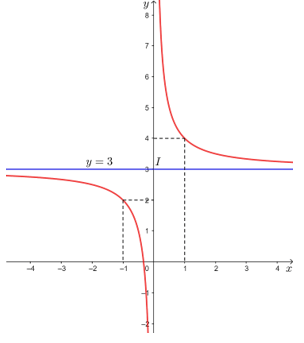
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.
Tâm đối xứng của đồ thị hàm số là điểm I(0; 3). Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 0 và y = 3.
b)
1. Tập xác định: D = ℝ\{1}.
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm y' = . Vì y' < 0 với mọi x ≠ 1 nên hàm số đã cho nghịch biến trên mỗi khoảng (– ∞; 1) và (1; + ∞).
● Tiệm cận:
Ta có . Suy ra đường thẳng y = – 1 là tiệm cận ngang của đồ thị hàm số.
Ta có . Suy ra đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
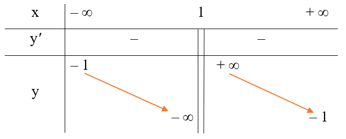
● Bảng biến thiên:
3. Đồ thị:
Ta có x = 0 thì y = – 3 nên đồ thị hàm số cắt trục Oy tại điểm (0; – 3).
Ta có y = 0 ⇔ ⇔ x = 3 nên đồ thị hàm số cắt trục Ox tại điểm (3; 0).
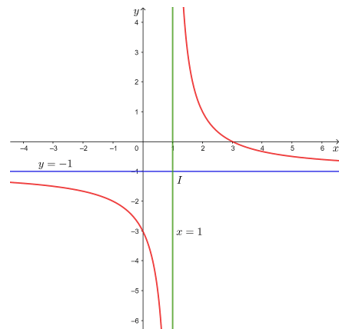
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.
Tâm đối xứng của đồ thị hàm số là điểm I(1; – 1). Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = – 1.
Cho hàm số y = – x2 + 4x – 3.
a) Lập bảng biến thiên.
b) Vẽ đồ thị của hàm số.
Khảo sát và vẽ đồ thị của các hàm số sau:
a) y = x3 + x – 2;
b) y = 2x3 + x2 – – 3.