Câu hỏi:
167 lượt xemKhảo sát và vẽ đồ thị của các hàm số sau:
a) y = – 2x3 – 3x2 + 1;
b) y = x3 + 3x2 + 3x + 2.
Lời giải
Hướng dẫn giải:
a) y = – 2x3 – 3x2 + 1
1. Tập xác định: ℝ.
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm y' = – 6x2 – 6x; y' = 0 ⇔ x = – 1 hoặc x = 0.
Trên các khoảng (– ∞; – 1) và (0; + ∞), y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.
Trên khoảng (– 1; 2), y' > 0 nên hàm số đồng biến trên khoảng đó.
● Cực trị:
Hàm số đạt cực đại tại x = 0 và yCĐ = 1.
Hàm số đạt cực tiểu tại x = – 1 và yCT = 0.
● Các giới hạn tại vô cực:
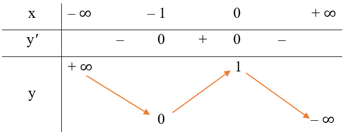
● Bảng biến thiên:
3. Đồ thị:
Khi x = 0 thì y = 1 nên (0; 1) là giao điểm của đồ thị với trục Oy.
Ta có y = 0 ⇔ – 2x3 – 3x2 + 1 = 0 ⇔ x = – 1 hoặc x =
Vậy đồ thị của hàm số giao với trục Ox tại hai điểm (– 1; 0) và
Điểm (0; 1) là điểm cực đại và điểm (– 1; 0) là điểm cực tiểu của đồ thị hàm số.
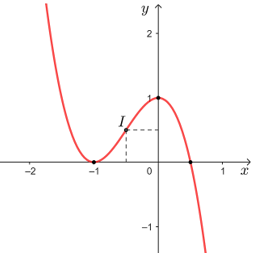
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.
Đồ thị của hàm số có tâm đối xứng là điểm I.
b) y = x3 + 3x2 + 3x + 2
1. Tập xác định: ℝ.
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm y' = 3x2 + 6x + 3 = 3(x + 1)2 ≥ 0 với mọi x ∈ ℝ;
y' = 0 ⇔ x = – 1.
Do đó, hàm số đồng biến trên khoảng (– ∞; + ∞).
Hàm số đã cho không có cực trị.
● Các giới hạn tại vô cực:
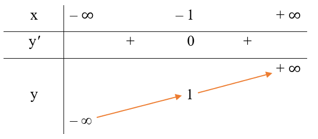
● Bảng biến thiên:
3. Đồ thị:
Khi x = 0 thì y = 2 nên (0; 2) là giao điểm của đồ thị với trục Oy.
Ta có y = 0 ⇔ x3 + 3x2 + 3x + 2 = 0 ⇔ x = – 2.
Vậy đồ thị của hàm số giao với trục Ox tại điểm (– 2; 0).
Đồ thị của hàm số đi qua các điểm (– 2; 0), (– 1; 1) và (0; 2).
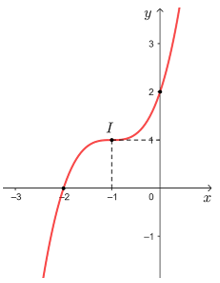
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.
Đồ thị của hàm số có tâm đối xứng là điểm I(– 1; 1).
Cho hàm số y = – x2 + 4x – 3.
a) Lập bảng biến thiên.
b) Vẽ đồ thị của hàm số.