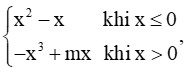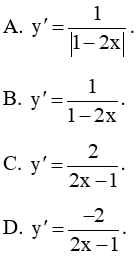Câu hỏi:
111 lượt xemLời giải
Hướng dẫn giải:
+) Với x < 0 thì f(x) = x2 – x. Có f'(x) = 2x – 1.
+) Với x > 0 thì f(x) = −x3 + mx. Có f'(x) = −3x2 + m.
Hàm số có đạo hàm tại mọi x ℝ khi và chỉ khi tồn tại f'(0).
Ta đi tính đạo hàm bên trái và đạo hàm bên phải tại điểm x = 0.
Có .
.
Do vậy hàm số có đạo hàm tại mọi x ℝ khi và chỉ khi m = −1.
Vậy m = −1 là giá trị cần tìm.
Câu 1:
Tự luận
Cho f(x) = cos2. Đạo hàm f'(0) bằng
A. 1.
B. −1.
C. 2cos.
D. -2cos.
1 năm trước
104 lượt xem
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 14:
Câu 15:
Câu 16:
Câu 17:
Câu 18:
Câu 19:
Câu 20:
Câu 21:
Câu 22:
Câu 24:
Câu 25:
Câu 26: