Câu hỏi:
72 lượt xemCho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC
Lời giải
Hướng dẫn giải:
|
GT |
ABC đều, G là trọng tâm của ABC |
|
KL |
G là trực tâm của ABC |
Chứng minh (Hình vẽ dưới đây):
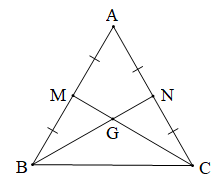
Gọi M, N theo thứ tự là trung điểm của AB và AC.
Vì tam giác ABC đều (giả thiết) nên AB = BC = CA.
Mà M là trung điểm của AB nên AM = BM.
Xét AMC và BMC có:
AC = BC (chứng minh trên),
MC là cạnh chung,
AM = BM (chứng minh trên).
Do đó AMC = BMC (c.c.c).
Suy ra (hai góc tương ứng).
Mà nên .
Do đó CM AB tại M.
Do đó CM là đường cao kẻ từ đỉnh C của tam giác ABC.
Chứng minh tương tự ta cũng có BN là đường cao kẻ từ đỉnh B của tam giác ABC.
Tam giác ABC có hai đường cao BN và CM cắt nhau tại G nên G là trực tâm của tam giác ABC.
Vậy G là trực tâm của tam giác ABC.
Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C
Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, = 25°. Tính và
