Câu hỏi:
83 lượt xem Tự luận
Cho tam giác nhọn ABC và điểm D nằm trong tam giác. Chứng minh rằng nếu DA vuông góc với BC và DB vuông góc với CA thì DC vuông góc với AB.
Lời giải
Hướng dẫn giải:
|
GT |
ABC nhọn, D nằm trong tam giác, DA BC, DB CA. |
|
KL |
DC AB. |
Chứng minh (Hình vẽ dưới đây):
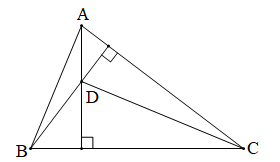
Tam giác ABC có DA BC, DB CA (giả thiết)
Mà DA cắt DB tại D nên D là trực tâm của tam giác ABC.
Do đó DC AB.
Vậy DC AB.
Câu 1:
Câu 2:
Câu 3:
Tự luận
Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C
1 năm trước
57 lượt xem
Câu 4:
Câu 5:
Câu 6:
Câu 7:
Câu 8:
Câu 10:
Tự luận
Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, = 25°. Tính và
1 năm trước
99 lượt xem
Câu 11:
