Câu hỏi:
67 lượt xem Tự luận
Chứng minh rằng nếu G là một đơn đồ thị có ít nhất hai đỉnh thì G có ít nhất hai đỉnh cùng bậc.
Lời giải
Hướng dẫn giải:
Giả sử G là một đơn đồ thị có n đỉnh (n ≥ 2).
Vì G là đơn đồ thị nên mỗi đỉnh của G không có khuyên và chỉ có thể nối với các đỉnh khác không quá một cạnh, nghĩa là mỗi đỉnh của G có bậc tối đa là (n – 1) (*).
Giả sử bậc của các đỉnh của G đều khác nhau. Khi đó bậc của n đỉnh của G lần lượt là 0, 1, ..., (n – 1), nghĩa là G phải có đỉnh bậc 0.
Do G có đỉnh bậc 0 nên các đỉnh khác của G có bậc tối đa là (n – 2) (mâu thuẫn (*)).
Vậy có ít nhất 2 đỉnh của G có cùng bậc.
Câu 1:
Câu 2:
Câu 3:
Câu 5:
Câu 6:
Tự luận
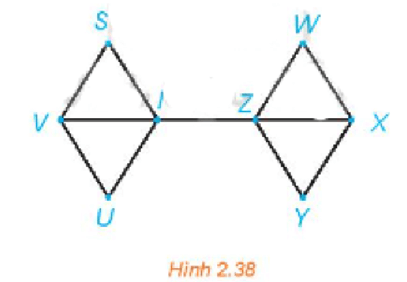
Hãy chỉ ra ít nhất 5 đường đi từ S đến Y trong đồ thị trên Hình 2.38.
1 năm trước
69 lượt xem
Câu 7:
Câu 8:
Câu 9:
Câu 10:
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 184 lượt thi