Câu hỏi:
79 lượt xemTìm số đỉnh nhỏ nhất cần thiết để có thể xây dựng một đồ thị đầy đủ với ít nhất 1 000 cạnh.
Lời giải
Hướng dẫn giải:
Giả sử G là một đồ thị đầy đủ có n đỉnh và có ít nhất 1 000 cạnh (n ∈ ℕ, n ≥ 2).
Vì G là đồ thị đầy đủ nên mỗi cặp đỉnh của G đều được nối với nhau bằng một cạnh, do đó mỗi đỉnh của G đều có bậc là (n – 1).
Tổng tất cả các bậc của các đỉnh của G là n(n – 1).
Suy ra G có số cạnh là (?(?−1))/2.
Vì G có ít nhất 1 000 cạnh nên ta có (?(?−1))/2≥1000
⇔ n(n – 1) – 2 000 ≥ 0
⇔ n2 – n – 2 000 ≥ 0 (*)
Giải bất phương trình (*), ta được ?≤(1−3 căn 889)/2≈−44,22 (không thỏa mãn) hoặc ?≥(1+3 căn 889)/2≈45,22 (thỏa mãn).
Do n là số tự nhiên nên n nhỏ nhất thỏa mãn là 46.
Vậy số đỉnh nhỏ nhất cần thiết để có thể xây dựng một đồ thị đầy đủ với ít nhất 1 000 cạnh là 46 đỉnh.
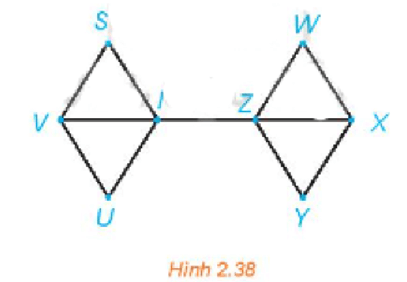
Hãy chỉ ra ít nhất 5 đường đi từ S đến Y trong đồ thị trên Hình 2.38.
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 194 lượt thi