Câu hỏi:
51 lượt xem
Lời giải
Hướng dẫn giải:
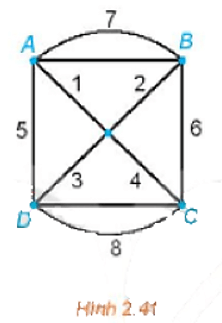
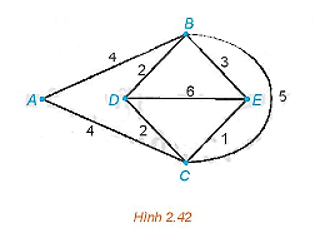
Vì đồ thị Hình 2.41 là liên thông và các đỉnh đều có bậc chẵn (ở đây đều là bậc 4) nên đồ thị có chu trình Euler.
Một chu trình Euler xuất phát từ đỉnh A là ABCDABDCA và tổng độ dài của nó là
7 + 6 + 8 + 5 + 7 + 2 + 3 + 8 + 4 + 1 = 51.
Vậy một chu trình cần tìm là ABCDABDCA và có độ dài là 51.
Câu 1:
Câu 2:
Câu 3:
Tự luận
Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 6.
10 tháng trước
45 lượt xem
Câu 4:
Câu 5:
Tự luận
Tìm số đỉnh nhỏ nhất cần thiết để có thể xây dựng một đồ thị đầy đủ với ít nhất 1 000 cạnh.
10 tháng trước
54 lượt xem
Câu 6:
Tự luận
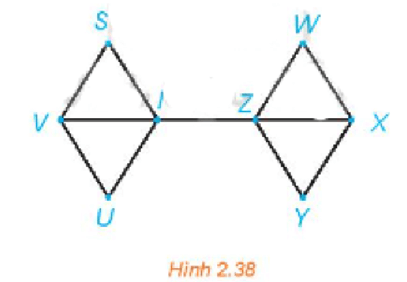
Hãy chỉ ra ít nhất 5 đường đi từ S đến Y trong đồ thị trên Hình 2.38.
10 tháng trước
59 lượt xem
Câu 7:
Tự luận
Kiểm tra xem các điều kiện của định lí Ore có thỏa mãn với các đồ thị trên Hình 2.39 không.
10 tháng trước
54 lượt xem
Câu 8:
Câu 10:
Tự luận
Giải bài toán người đưa thư với đồ thị có trọng số trên Hình 2.42.
10 tháng trước
66 lượt xem
ĐỀ THI LIÊN QUAN:
-
34 câu hỏi 142 lượt thi